It's not a pedal triangle!

Geometry Level 4

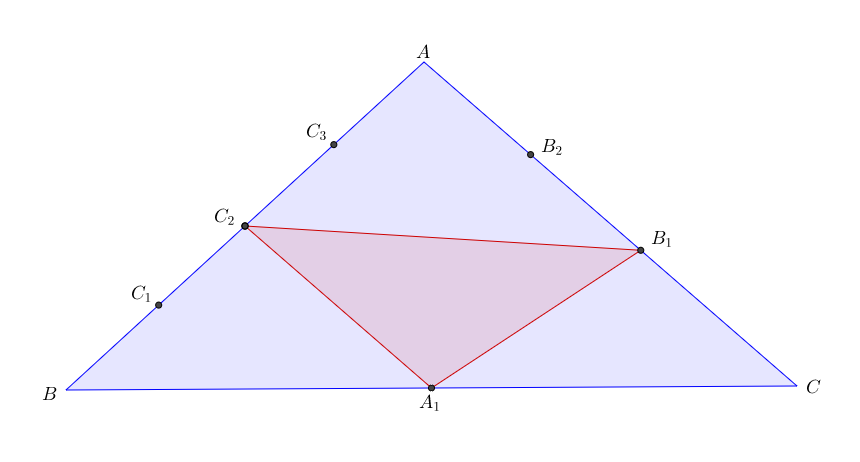
In the figure given above (for illustration purposes only), points $A_1$ , $(B_1, B_2)$ , $(C_1, C_2, C_3)$ are taken on sides $BC$ , $CA$ and $AB$ of $\Delta ABC$ respectively such that

$A_1$ is the mid-point of $BC$ ;
$B_1$ and $B_2$ are the points of trisection of $CA$ ;
$C_1$ , $C_2$ and $C_3$ divide the segment $AB$ into four equal parts

A triangle $\Delta A_1 B_1 C_2$ is constructed with vertices at $A_1$ , $B_1$ and $C_2$ .

Find $\dfrac{\text{Area } \Delta ABC}{\text{Area } \Delta A_1 B_1 C_2}$ .

The answer is 4.000.

2 solutions

Marta Reece
Mar 24, 2017

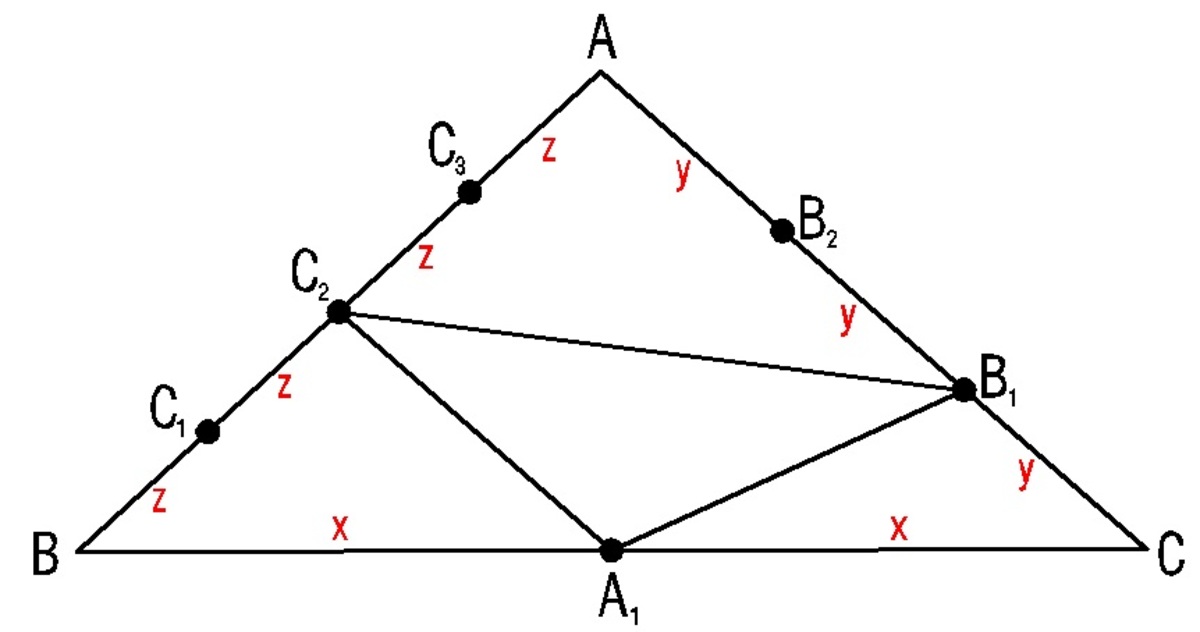
Points $A_1$ and $C_2$ are midpoints of their respective sides, therefore $A_1C_2$ is parallel to $AC$ and $A_1C_2=\frac{1}{2}AC$ .

It's easy to see that area of $A_1C_2B_1$ would be $\frac{1}{4}$ of area of $ABC$ if $B_1$ was also a midpoint (similar triangles with sides half the size).

However the fact that $B_1$ is not a midpoint does not matter, because the vertical distance between any point on line $AC$ and $A_1C_2$ is the same, so the ratio of the areas remain the same as well.

A Former Brilliant Member
Mar 24, 2017

Splendid solution. Just what I was expecting! (+1)

I did it via coordinate geometry.

Tapas Mazumdar - 4 years, 2 months ago

No need of such works. Use the fact that Ar. AA1C2 = 1/4 ABC. But Tri. AA1C2 and A1B1C2 are on the same base and between the same parallel line AB and A1C2. Therefore, area triangle $A1B1C2$ = $AA1C2$ = 1/4 ABC. Done.

Vishwash Kumar ΓΞΩ - 4 years, 2 months ago

It's not a pedal triangle!

The answer is 4.000.

2 solutions

0 pending reports