Its not a triangle. It's not a sector. It's a Trianglector!
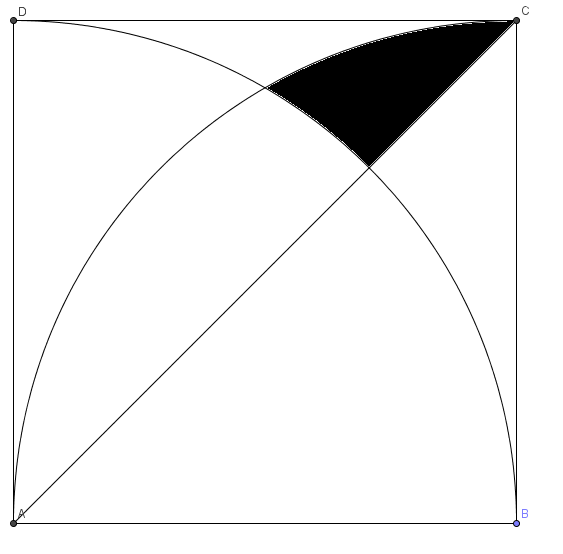 Square
has side length
. The quarter-circle sectors
and
are drawn, along with diagonal
. If the area of the shaded region is
, where
are all integers with
not divisible by the square of any prime and
, find
.
Square
has side length
. The quarter-circle sectors
and
are drawn, along with diagonal
. If the area of the shaded region is
, where
are all integers with
not divisible by the square of any prime and
, find
.
The answer is 766.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Reference this diagram .
I will refer to the area obtained by removing the triangle portion of a sector as a segment . Note that the desired area is the area of the segment of the large quarter circle containing the desired area, minus the red and green regions. The red region is a segment of a sector of measure 60 degrees (since E B = A B = A E which implies that △ E A B is equilateral), and the green region is a sector of measure 15 degrees. The larger segment is a portion of a sector of 90 degrees.
Area of the Red Region
The area of the red region is 6 1 ( π ) − 4 3 . (A 60-degree sector with radius 1 minus the area of an equilateral triangle with radius 1.)
Area of the Green Region
The area of the green region is 2 4 1 ( π ) . (A 15-degree sector with radius 1.)
Area of the Quarter-Circle Segment
The area of the quarter circle segment is 4 1 ( π ) − 2 1 . (A 90-degree sector with radius 1 minus the area of an isosceles right triangle with leg length 1.)
Area of the Desired Region
This is equal to the area of the quarter-circle segment minus the sum of the areas of the red region and the blue region.
4 1 ( π ) − 2 1 − ( 6 1 ( π ) − 4 3 + 2 4 1 ( π ) )
I'll save you the simplification and tell you that the desired answer comes out to 2 4 π − 1 2 + 6 3 , from which the desired answer is 1 2 + ( − 1 2 ) 2 + 6 2 + 3 2 + 2 4 2 = 7 6 6 .