Imagine the square as being made of 4 overlapping semicircles.
Area of 4 semicircles = 2πr^2 = 2×3.14×100 = 628cm^2.
Area of the square = 20×20cm = 400cm^2.
Area of the shaded region= Area of the four semicircles - Area of the square= 228cm^2

The square consists of 4 blue parts and 4 white parts

It is easy to prove that the 4 blue parts are congruent and the 4 white are

congruent

Let the area of one blue part is denoted by x

Let the area of one white part is denoted by y

Area of the square = 400 = 4x + 4y

x + y = 100 ....................................... (1)

area of one semicircle = (1/2) Pi (10)^2 = 2x + y

2x + y = 157 .....................................(2)

From (1), (2) we get

x = 57

Then

Then required area = 4(57) = 228

Let us Mark the four un-shaded regions as I, II, III and IV.

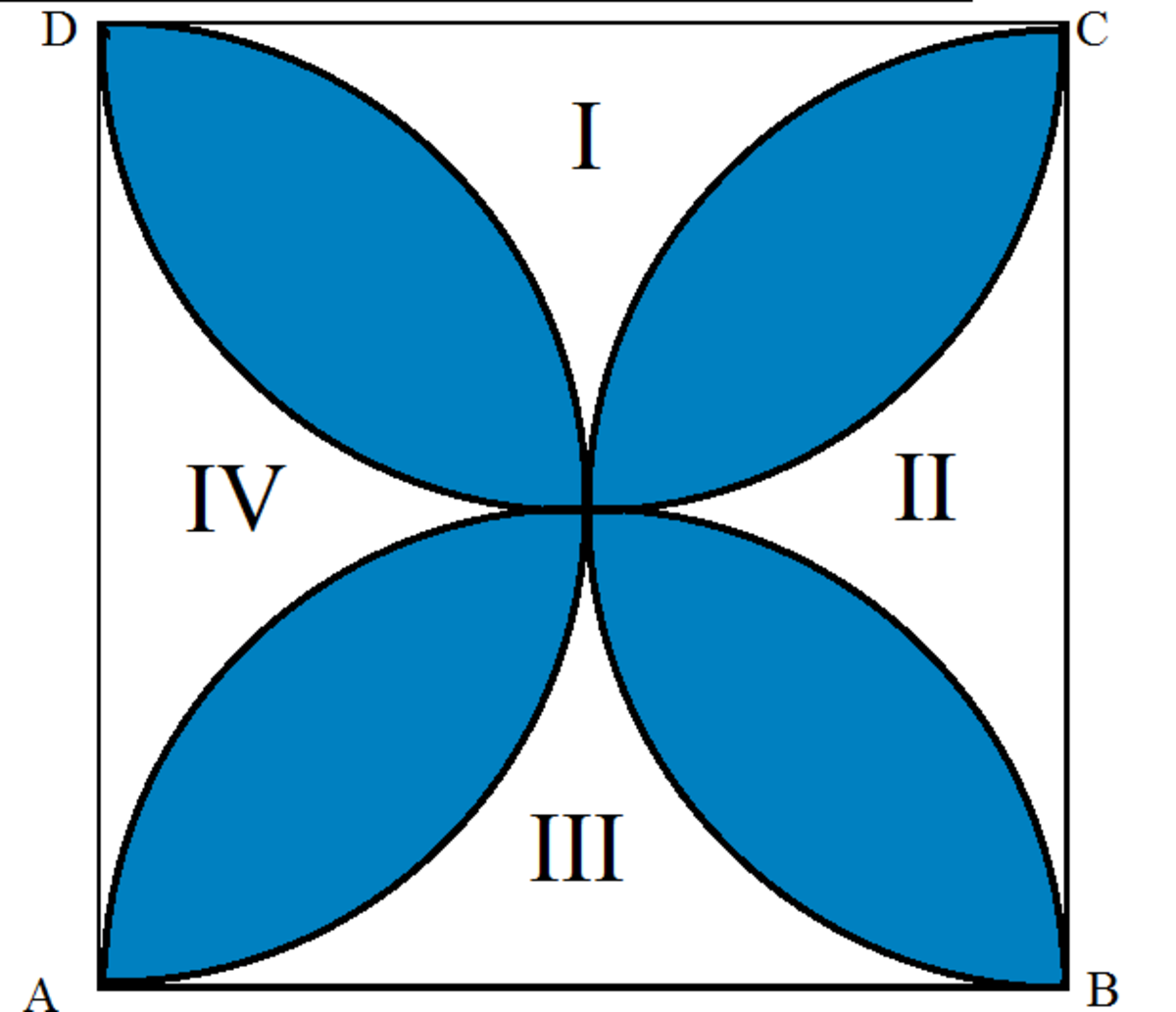
The Total Area of the portions I and III =

Total Area of Square ABCD - area of semi-circle with diameter BC - area of semicircle with diameter AD

Area of Square = (20*20) cm^2 = 400 $cm^{2}$

Radius = 10 cm.

=[20 20 - (3.14 10^2 )/2 - (3.14*10^2)/2] $cm^{2}$

=[400 - 157 - 157] $cm^{2}$

=86 $cm^{2}$

Similarly, the area of Portions II and IV = 86 $cm^{2}$

Therefore Total Area of the Shaded Portion = Area of Square - Sum of Area of the shaded Portions ( Area ofI, II, III and IV)

Sum of Unshaded Portion = (86 +86) $cm^{2}$ = 172 $cm^{2}$

Area of Shaded Portion = (400 - 172) $cm^{2}$

Area of The Shaded Portion = $\boxed{228}$ $cm^{2}$

First, find the area of the square, then imagine there is a ball/circle inside the square, afterwards find the area of the ball

Area of the square :
(S x S) ===> 20 x 20 = 400 cm^2

Area of the ball/circle:
(πr^2) ===> 3,14 x 10 x 10 = 314 cm^2

the inner and the outer area(white area) of the ball has the same broad. to determine the extent of its area, find outer area first, then multiply it by 2 (because they has the same broad)

Area of the square - area of the circle: 400 - 314 = 86 cm^2 then multiply it by two: 86 x 2 = 172 cm^2 so the inner + outer area is 172 cm^2

finally got the blue area by: Area of square - the inner n outer area of the ball (white area): 400 - 172 = 228 cm^2

The thing I love about calculus is that it works even if you're bad at geometry. This integral can be used to calculate the area of one "petal"... Multiply the answer by 4.

.

* The blank area outside the circle is obviously the same as the blank area inside the circle.

>>if the complete square is 20x20= 400cm2 we can substract 86 cm2 for the blank area outside of the circle and then another 86cm2 for the blank area inside ;)

400-86-86=228

My solution is ( i dont know if it will be worth to, because im just a common student, please do correct mine if i were wrong): 1. Cut the pic and take it into a quarter of square. 2. Then use the area of the semicircle and minus it to the area of the triangle.

3. You will get a 1/8 of its overlapping semicircle so you have to times 8.

1. (Nth to count)
2. Area of the semicircle = 1/4 πr^2 = 1/4 3.14 10^2 = 78.5 Area of a quarter of triangle= 1/2 lh = 1/2 10 10 = 50 Then , minus it and you will get a result of 28.5
3. Lastly you need to do is 28.5 x 8 = 228cm^2

Square - (Square - Circle) - (Square - Circle) = 2*Circle - Square

Isolate one quadrant of a circle...divide the shaded portion into 2 areas, making one circular segment.. Hence its area = r^2/2 ( theta - Sin theta )..The total area will be multiplied by 8...hence A = 8 x 10^2 /2 ( pi/2 -1 ) = 228 cm^2...note..theta = pi/2 radians and sin pi/2 =1

There is one square and 4 semicircles overlapping. If we consider one semicircle, it contains two shaded regions. And one shaded region is common between two shaded regions. So, if we calculate the area of all semicircles and add them, it will be: 4 ( (π * r^2)/2) = 628 sq cm. (Since all semicircles are of same radius) This area is nothing but: Area of unshaded region + 2 Area of shaded region And, area of square is nothing but: Area of unshaded region + Area of shaded region. So, if we subtract area of sqaure, which is 20*20 = 400 sq cm. from area of all semicircles, we will get our desired answer. Area of shaded region = 628 - 400 = 228 sq cm. Yay :)