Graphing Prevents Overthinking
There are four lines that are tangent to both circles
x
2
+
y
2
=
1
and
(
x
−
6
)
2
+
y
2
=
4
.
What is the sum of the slopes of these four lines?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Exactly how I solved it.
That is a good logic. But i uploaded a mathematical solution.
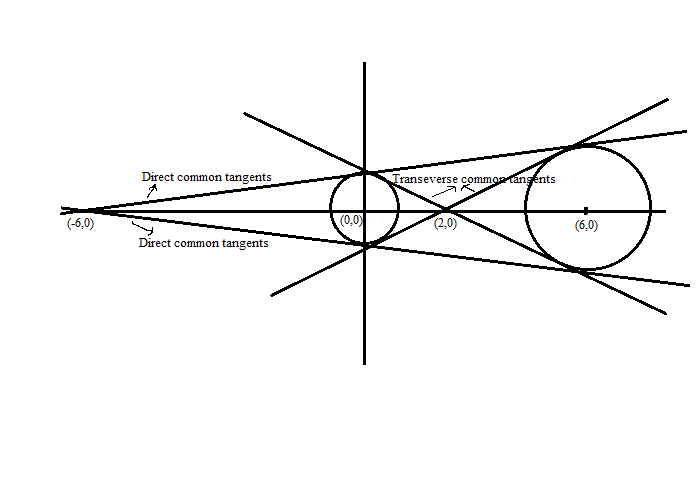
The combined equation of direct common tangents comes out to be x 2 − 3 5 y 2 + 1 2 x + 3 6 = 0 and that of transverse common tangents comes out to be x 2 − 3 y 2 − 4 x + 4 = 0 . The sum of slopes of DCT and TCT is 0 because there is no term of x y in their combined equations. Hence, the answer is 0 .
Looks like you go CatalyseR
Log in to reply
Yes, this problem appeared in CatalyseR's test series.
Is there any direct formula for finding combined equation of DCT and TCT?
Log in to reply
No, there's no direct formula. You have to find them by method. If you want i can upload the method.
Log in to reply
It seems quite obvious that graph would be symmetric about x-axis so sum of slopes would be 0.
Yes please upload the method for finding DCT and TCT
The center of both circles lie on the x-axis, so the slopes of the two tangents that are common to both circles are the negation of each other.