It's not that Irodov problem number 3.24
A cube of side length is placed such a way in space such that its main body diagonal is -axis and other perpendicular axis are and . The origin is at the body center of cube. An electric field is defined in a space such that . Find the electric flux through cube due to this field, where SI units.
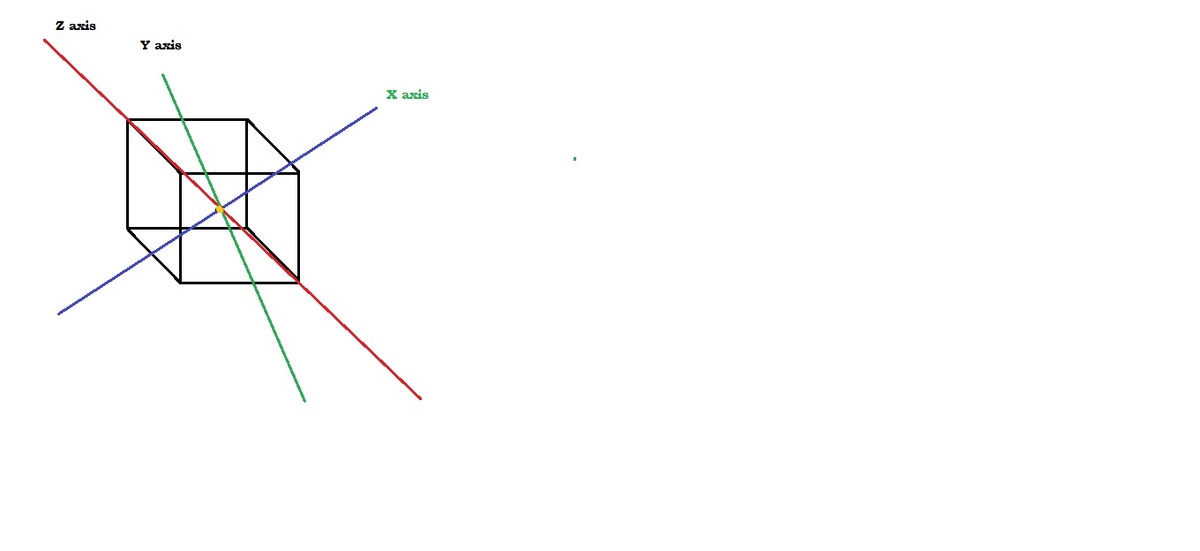
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A very close look to the electric field configuration makes it clear that this electric field is due to a infinite charged line placed along z axis