It's okay to be a tangent

Geometry Level 4

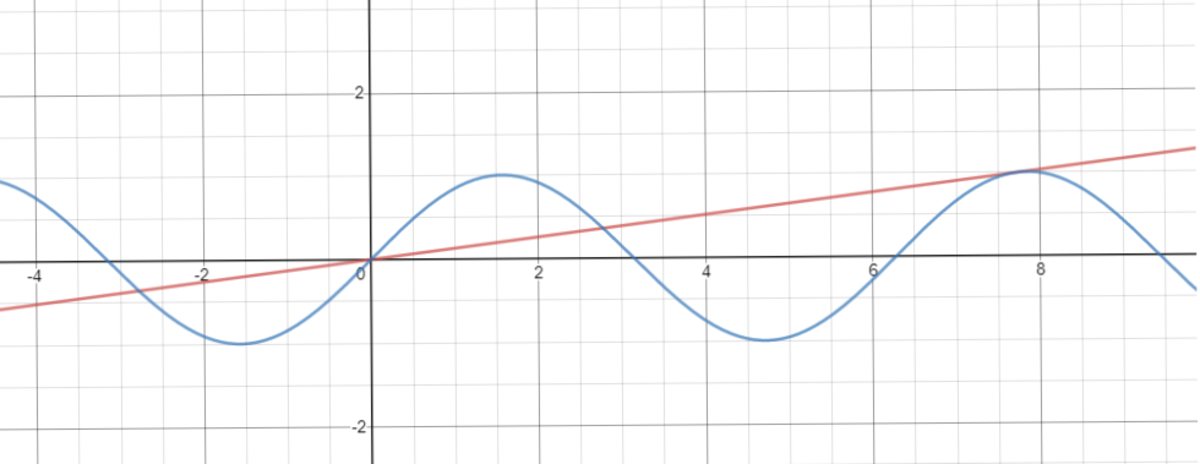The given graph is of a sine function. What must be the slope of straight line passing from the origin to just touch the second crest as seen in the graph? Round your answer to three decimal places. Also refrain from using graphing calculator.


The answer is 0.128.

Hitesh Yadav by Hitesh Yadav , 16, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Numerical technique has to be used in this problem. Let the point of tangency be ( h , sin ⁡ h ) (h, \sin h)

Slope of the tangent is cos ⁡ h \cos h (through differentiation)

So, cos ⁡ h = sin ⁡ h h ⟹ h = tan ⁡ h \cos h=\dfrac {\sin h}{h}\implies h=\tan h

where 2 π < h < 2.5 π 2π<h<2.5π

Solution to this equation is numerically obtained as h ≈ 7.72 5 c h\approx 7.725^c

Therefore the required slope is cos ⁡ h ≈ 0.128 \cos h\approx \boxed {0.128} .

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...