An algebra problem by Tanishq Varshney

Substitute $t = x^2$ results in this equation:

$t^2 + (1-2k)t + k^2 - 1 = 0$

For the original equation to have four real roots, the resultant equation must have two distinct positive real roots $t_1$ and $t_2$ . $t_1$ and $t_2$ are both positive if and only if their sum and their product are positive.

The conditions are as follows:

$\begin{array}{l} \left\{ \begin{array}{l} \Delta = {(1 - 2k)^2} - 4({k^2} - 1) = - 4k + 5 > 0 \\ {t_1} + {t_2} = - (1 - 2k) > 0 \\ {t_1}{t_2} = {k^2} - 1 > 0 \\ \end{array} \right. \\ \left\{ \begin{array}{l} k < \displaystyle\frac{5}{4} \\ k > \displaystyle\frac{1}{2} \\ k < - 1 \vee k > 1 \\ \end{array} \right. \\ \left\{ \begin{array}{l} k < \displaystyle\frac{5}{4} \\ k > 1 \\ \end{array} \right. \\ \end{array}$

Hence, $k \in \left( {1,\displaystyle\frac{5}{4}} \right)$

Note that $x^4 + (1-2k)x^2 + k^2 - 1 = 0$ is a quadratic equation of $x^2$ . Solving the quadratic, $x^2 = \dfrac {2k-1 \pm \sqrt{(2k-1)^2-4(k^2-1)}}2 = \dfrac {2k-1\pm \sqrt{5-4k}}2$ . $\implies x = \pm \sqrt{\dfrac {2k-1\pm \sqrt{5-4k}}2}$ . For real root $x$ ,

$\begin{aligned} \frac {2k-1\pm \sqrt{5-4k}}2 & \ge 0 \\ 2k-1 - \sqrt{5-4k} & \ge 0 \\ 2k-1 & \ge \sqrt{5-4k} & \small \color{#3D99F6} \text{Squaring both sides} \\ 4k^2 -4k + 1 & \ge 5-4k \\ 4k^2 & = 4 \\ \implies k & \ge 1 & \small \color{#3D99F6} k=-1 \text{ is not acceptable.} \end{aligned}$

Note also that $x = \pm \sqrt{\dfrac {2k-1\pm \sqrt{5-4k}}2}$ is real only when $\sqrt{5-4k}$ is real or $5-4k \ge 0$ , $\implies k \le \dfrac 54$ .

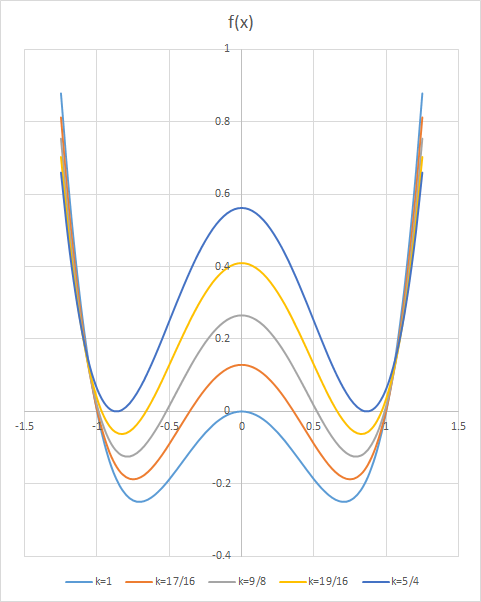
Therefore, the equation has real roots when $k \in \left[1,\frac 54\right]$ . We note that the equation $f(x) = x^4 + (1-2k)x^2 + k^2 - 1$ is an even function with a local maximum at $x=0$ and two equal minima at $\pm x_a$ . This can be shown by equating $f'(x) = 4x^3 + 2(1-2k)x = x(4x^2-4k+2) = 0$ . $\implies x = 0$ and $x_a = \pm \sqrt{k-\frac 12}$ . $f''(x)=12x^2 - 4k+2$ , $f''(0) < 0$ , $\implies f(0)$ is a local maximum. $f''(x_a) = 12k-6-4k+2 = 8k - 4 > 0$ for $k \ge 1$ , $\implies f(\pm x_a)$ are minima. Function $f(x)$ is therefore a W-shaped curve symmetrical about the $y$ -axis. As $k$ increase from 1 to $\frac 54$ , the curve moves upward.

When $k=1$ , $f(x) = x^4-x^2 = x^2(x-1)(x+1) = 0$ has only three roots $-1,0,1$ . This is because the maximum at $x=0$ is touching the $x$ -axis. For $k > 1$ , then $f(x)$ will have four roots.

When $k = \frac 54$ , $f(x) = x^4-\frac 32 x^2 + \frac 9{16}= \left(x^2 - \frac 34\right)^2 = 0$ has only two roots $\pm \frac {\sqrt 3}2$ . This is because the two minima at $\pm x_a = \sqrt{k-\frac 12} = \sqrt{\frac 54 - \frac 12} = \frac {\sqrt 3}2$ are touching the $y$ -axis. For $k < \frac 54$ , then $f(x)$ will have four roots.

Therefore, $f(x)$ has four real roots when $k \in \boxed{\left(1, \dfrac 54\right)}$ .