it's pretty. Geometrical probability
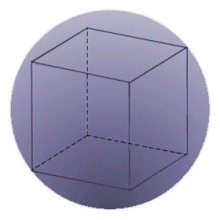 A cube is circumscribed in a sphere. What is the probability that a point (taken randomly) lies inside the sphere, but outside the cube.
A cube is circumscribed in a sphere. What is the probability that a point (taken randomly) lies inside the sphere, but outside the cube.
If the answer is of the form , then what is the value of . (rounded off up to 3 decimal places)
You can try my other Probability problems by clicking here
The answer is 2.721.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Assume that the cube has a length of x . Therefore, its volume is x 3 . Using the Pythagorean Theorem, one can see that the diagonal of one side of the cube is 2 x and the diagonal from one vertex of the cube to the opposite vertex is 3 x . This is equivalent to the diameter of the sphere.
The radius of the sphere is 2 3 x . The volume of a sphere is 3 4 π r 3 . Using this formula, the volume of the sphere in the problem is 2 3 π x 3 .
To find the probability of a point being inside the cube given that we know it is inside the sphere, we simply need to divide the volume of the sphere: 2 3 π ( x 3 ) by the volume of the cube: x 3 or 2 3 π x 3 x 3 = 2 3 1 π
We now know the probability of a point being inside the cube given that we know it is inside the sphere. However, we want to find the probability of the point not being in the cube, given that it is inside the sphere. This would be the total probability minus the answer we found, or ...
1 − 2 3 π 1 .
λ = 2 3 π . This can be approximated to 2 . 7 2 1 on a calculator.