Surface tension of a water bubble
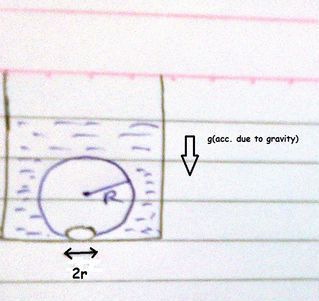
When we heat water in a vessel, air bubbles are formed at the bottom. These bubbles detach from the base and rise.
Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If r < < R , and the surface tension of water is T .
If the density of water is ρ , find the value of r just before the bubbles detach.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
If I go on with actual solution , then
Surface tension force

Now, Buoyancy Force : F = V i ρ g
Volume can be calculated by using volume of dome's formula V = 3 π h 2 ( 3 R − h )
But in this case due to the approximation , everything goes neglected and you end up with volume of sphere's formula .
These two forces balance each other !
Can you please check my solution and tell what's incorrect?
Log in to reply
Nothing is incorrect , actually first we should calculate the volume of dome and at end when we will apply condition that r,<<R we will land on volume of sphere !
