It’s scandalous! #2
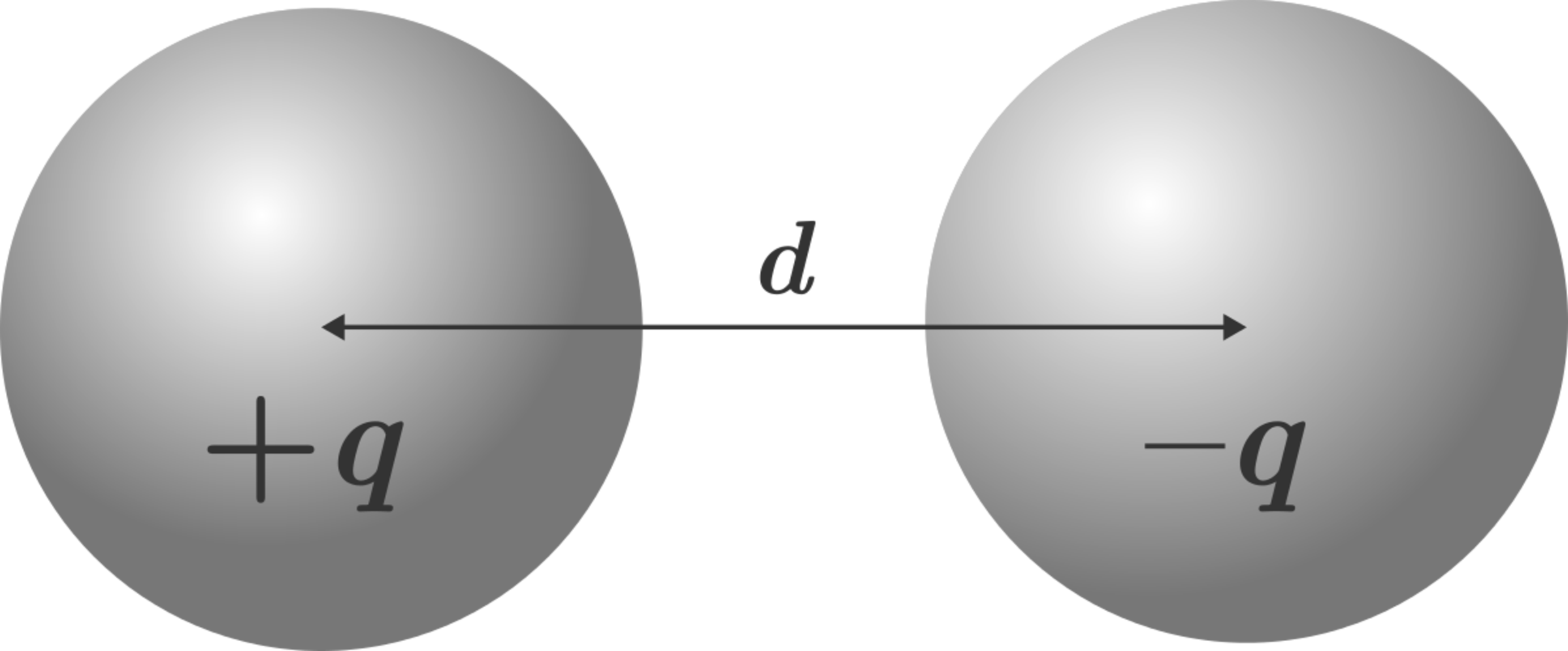
Two small conducting spheres of equal radius have charges of C and C.
Case 1: The force experienced by them if placed 4 cm apart = A .
Case 2: If they are brought into contact, and then separated by 4 cm, the force between them = B .
A _ B. The nature of B is _
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If by "spheres" the problem writer means "balls," then the force of attraction between the two balls is given by the product of 4 π ϵ 0 q 1 q 2 and a sextuple integral that I do not wish to take the time to express, assuming the charge is spread evenly across the balls. In both cases, the sextuple integral is the same. The only things that change are q 1 and q 2 . The charges are unlike to begin with so the force is attractive. My belief is that, when the balls touch, the charges average out. So, B A = ( 2 0 . 6 × 1 0 − 1 9 + − 8 × 1 0 − 1 9 ) ( 2 0 . 6 × 1 0 − 1 9 + − 8 × 1 0 − 1 9 ) 0 . 6 × 1 0 − 1 9 × − 8 × 1 0 − 1 9 ≈ − 0 . 3 5 0 6 . Therefore, force B is repulsive and greater in magnitude than force A . Scandalous indeed.