It's so cute!
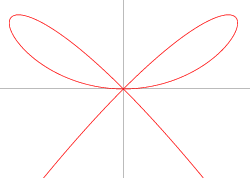 The graph above satisfy the equation
x
4
+
y
3
=
x
2
y
.
The graph above satisfy the equation
x
4
+
y
3
=
x
2
y
.
The area enclosed by the 2 cute adorable little fine loops is equals to b a for coprime positive integers a and b . What is the value of a + b ?
The answer is 113.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Very nice solution Pranav! (y)
It looks like Brilliant has deleted my solution. It's just a joke. Seemly, no one here has sense of humour. I thought I could have fun here. Ckckck...
Log in to reply
Thank you Fey! :)
I am sorry to hear about the deletion of your solution. :(
If you have some time, can you please have a look at my comment on your solution to this: Plenty of integrate by Part 2 . It would be appreciated, thanks!
Log in to reply
Maybe this link could help you answer your question: Sinc Function . See equation (37). :)
nice solution thanks
Convert the equation from Cartesian to Polar coordinates. Integrate with limits of 0 to Pi/4 in polar coordinates area and you get a=8 & b=105. Therefore, a+b=113
I tried polar first since it looked like a polar graph haha but I got the identities mixed up so the integral wasn't too clean.
Another way that I found is by parametrizing the curve using the usual y = t x . Plugging in, we get x 4 + x 3 t 3 = x 2 ( x t ) whence, x = t − t 3 and y = t 2 − t 4 for t ∈ R
Since we want the area of two copies of the loop in the first quadrant, we solve x = y = 0 and get the first positive solution for t , which is 1 . We get the area by integrating about the first loop using Green's Theorem
2 A = 2 ⋅ ( 2 1 ∮ C x d y − y d x )
= ∫ 0 1 ( t − t 3 ) ( 2 t − 4 t 3 ) − ( t 2 − t 4 ) ( 1 − 3 t 2 ) d t
= 1 0 5 8
This problem can be easily solved if one uses polar coordinates.
Substitute x = r cos t and y = r sin t . I am using t instead of θ . The equation changes to:
r cos 4 t + sin 3 t = cos 2 t sin t
⇒ r = tan t sec t ( 1 − tan 2 t )
Before setting up the area integral, we need to find the limits for integration. Substitute r = 0 to get t = 0 and t = π / 4 .
The area bounded by the curve is hence
A = 2 × ( ∫ 0 π / 4 2 1 r 2 ( t ) d t )
⇒ A = ∫ 0 π / 4 tan 2 t sec 2 t ( 1 − tan 2 t ) 2 d t
The above integral can solved by using the substitution tan t = x and comes out to be:
A = 1 0 5 8