It's so easy for summation

We first simplify the general term as follows:

$\sin(n^\circ)\cos(n^\circ)\tan(n^\circ)=\frac{\sin(n^\circ)\cos(n^\circ)\sin(n^\circ)}{\cos(n^\circ)}=\sin^2(n^\circ)$

Now, we use the identity $\sin(90^\circ-A^\circ)=\cos(A^\circ)$ to rewrite our sum along with the simplified form of general term obtained. We also use the identity $\sin^2\theta+\cos^2\theta=1~\forall~\theta\in\Bbb{R}$ which also works for $\theta$ in degrees since they are real when expressed in radians. Call the sum $S$ . We get,

$S=\sum_{n=1}^{89}\sin^2(n^\circ)=\left(\sum_{n=1}^{44}\left(\sin^2(n^\circ)+\cos^2(n^\circ)\right)\right)+\sin^2(45^\circ)\\ \implies S=\left(\sum_{n=1}^{44}1\right)+\frac{1}{2}=44\times 1+\frac{1}{2}=44.5$

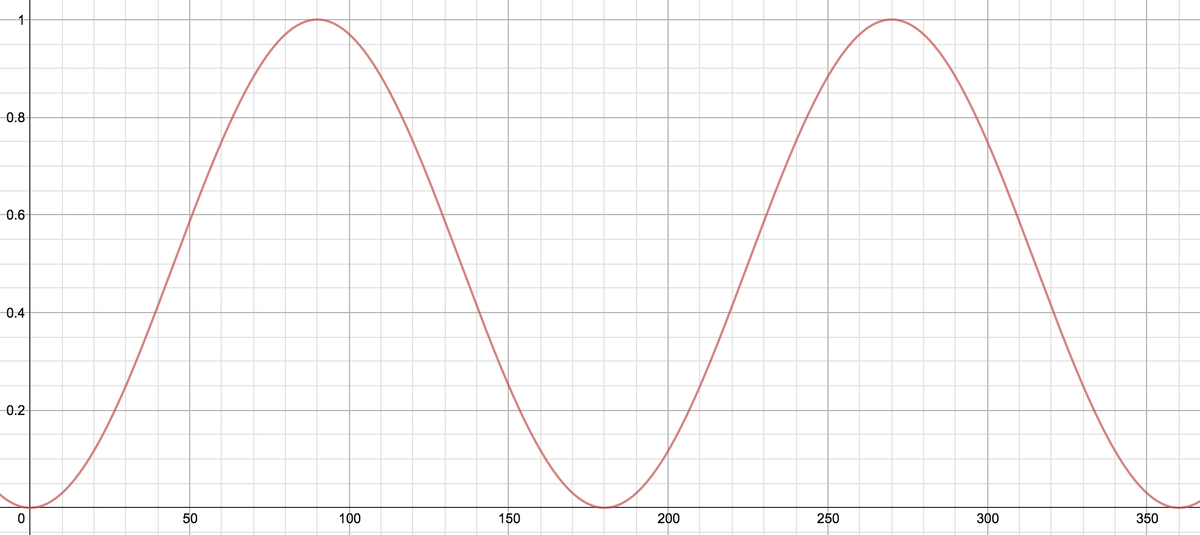
As others have noted, $\sin n^{ \circ }\cos n^{ \circ }\tan n^{ \circ }=\sin ^{ 2 } n^{ \circ }$ .

What does $\sin ^{2} n^{\circ}$ look like? See below.

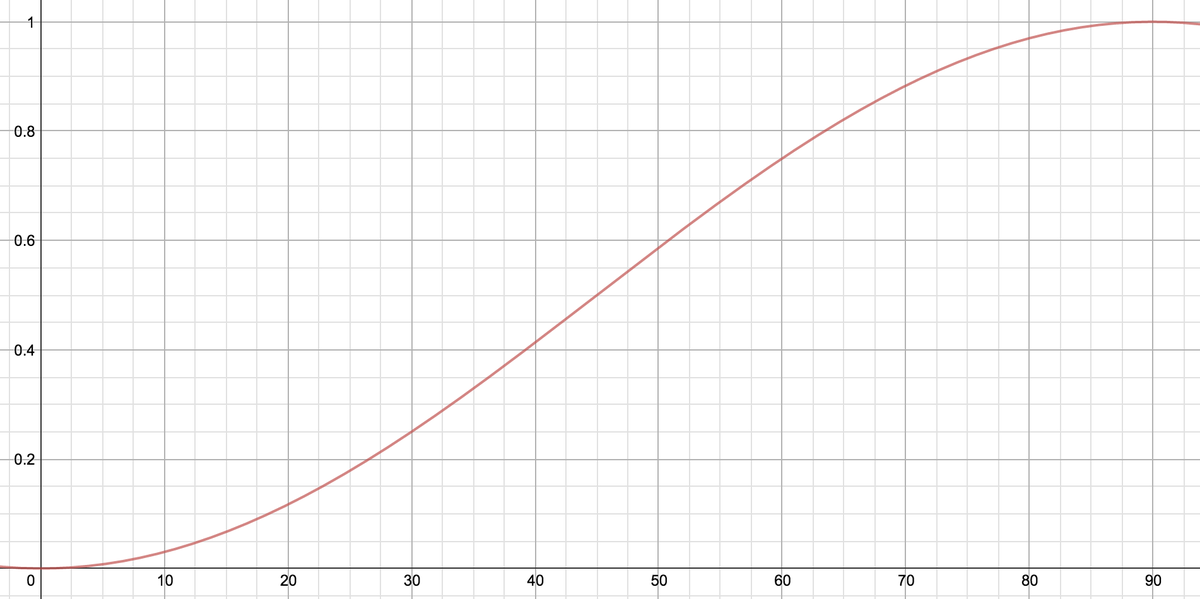
But we're interested in the interval from $n^{\circ} = 1$ to $n^{\circ} = 89$ :

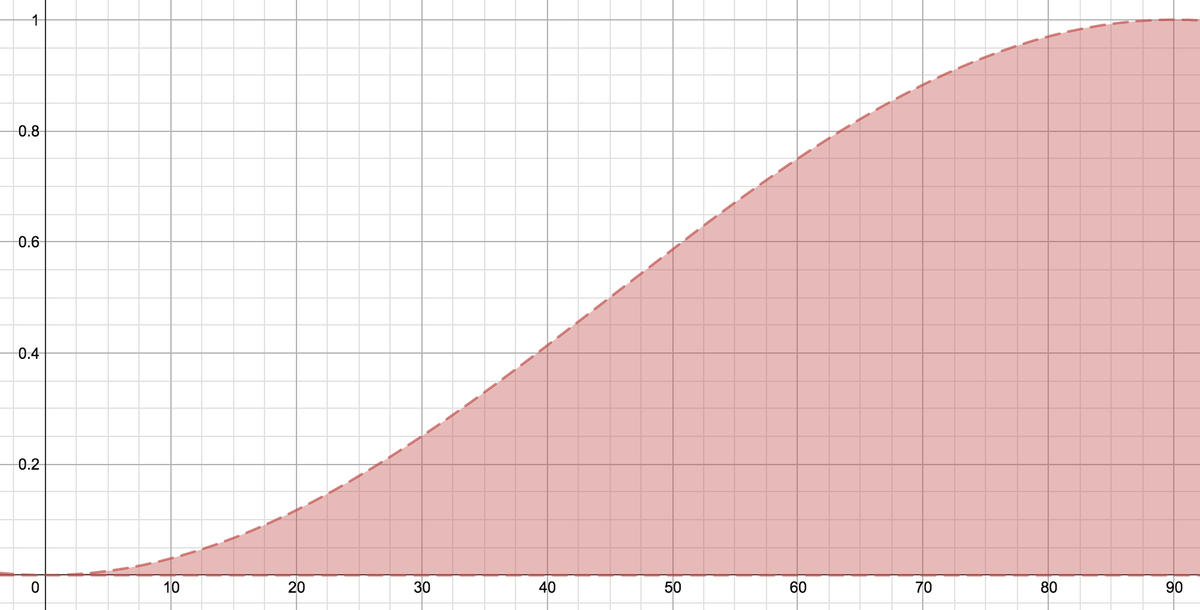
The summation is similar to the following integral:

... which is equal to the area of this rectangle:

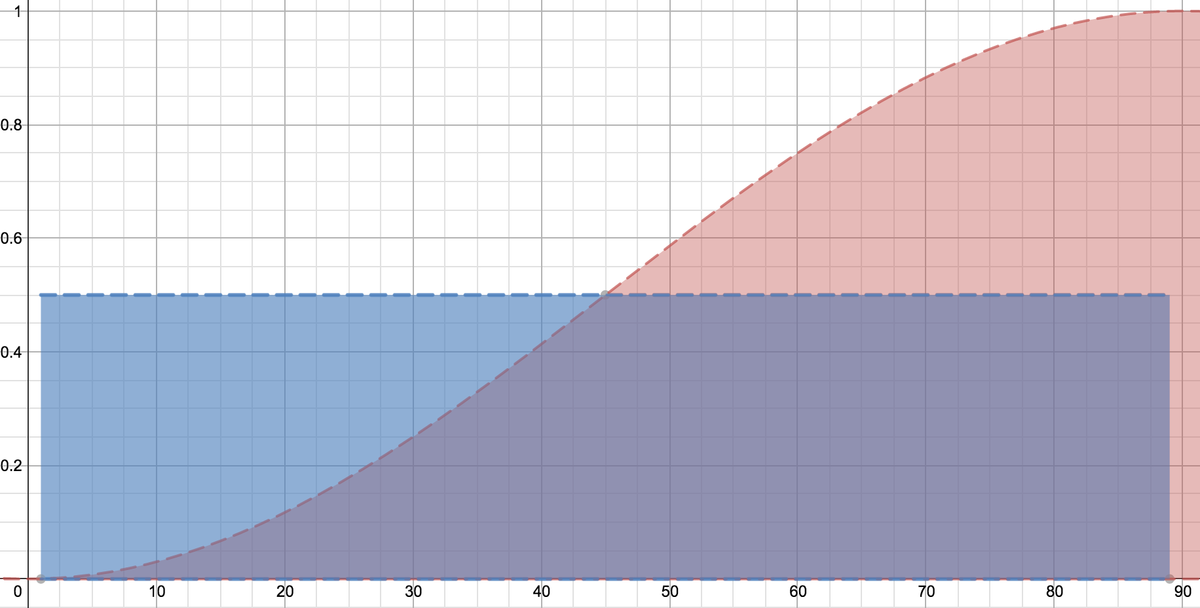
... which has an area of $0.5 \times 90 = 45$ .

sin n *cos n * tan n = sin n * sin n

sin 1=cos 89

sin n * sin n+cos n * cos n =1

sin 45* sin 45=0.5

Using these you can get answer