It's swimming time!
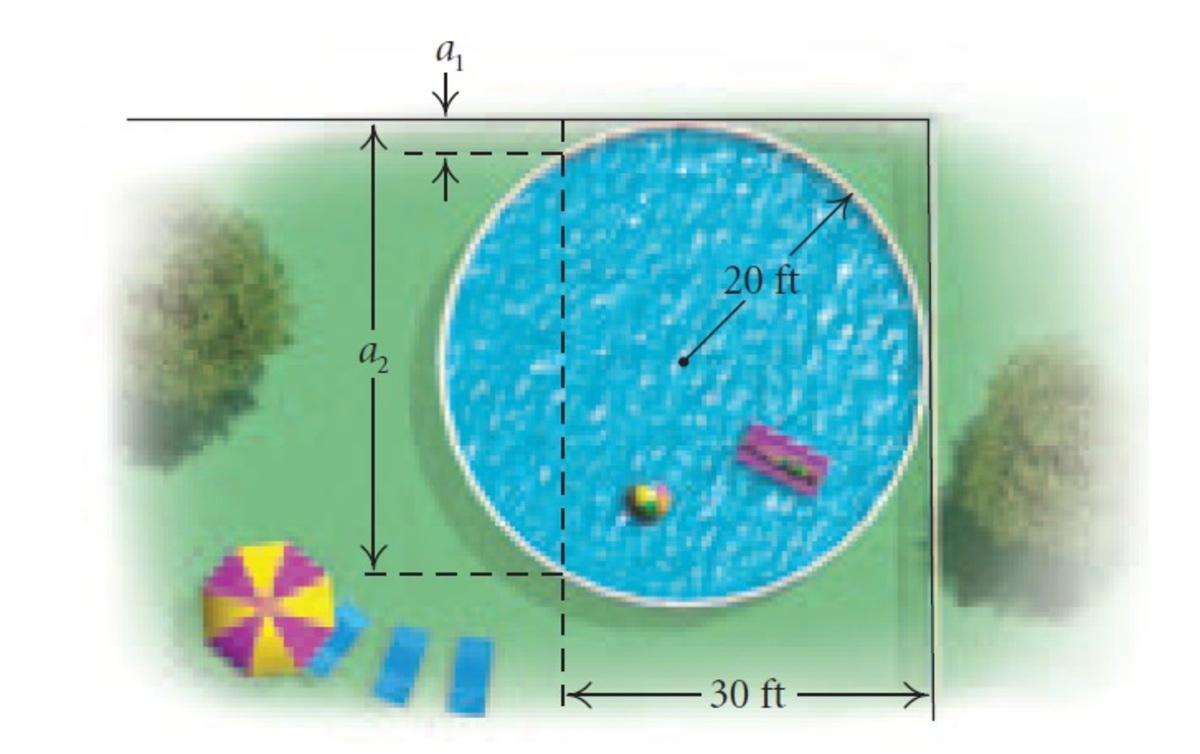A swimming pool in the shape of a circle (as shown above) is to be built in a corner of a square. Before the construction begins, the contractor must know the values of
a
1
and
a
2
. If you are the contractor, what is
a
1
+
a
2
?
Details:
-
2 0 feet is the radius of the circle.
-
Both a 1 and a 2 are perpendicular to one side of the square.
-
Give your answer in feet.
-
The swimming pool touches the two sides of the square.
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
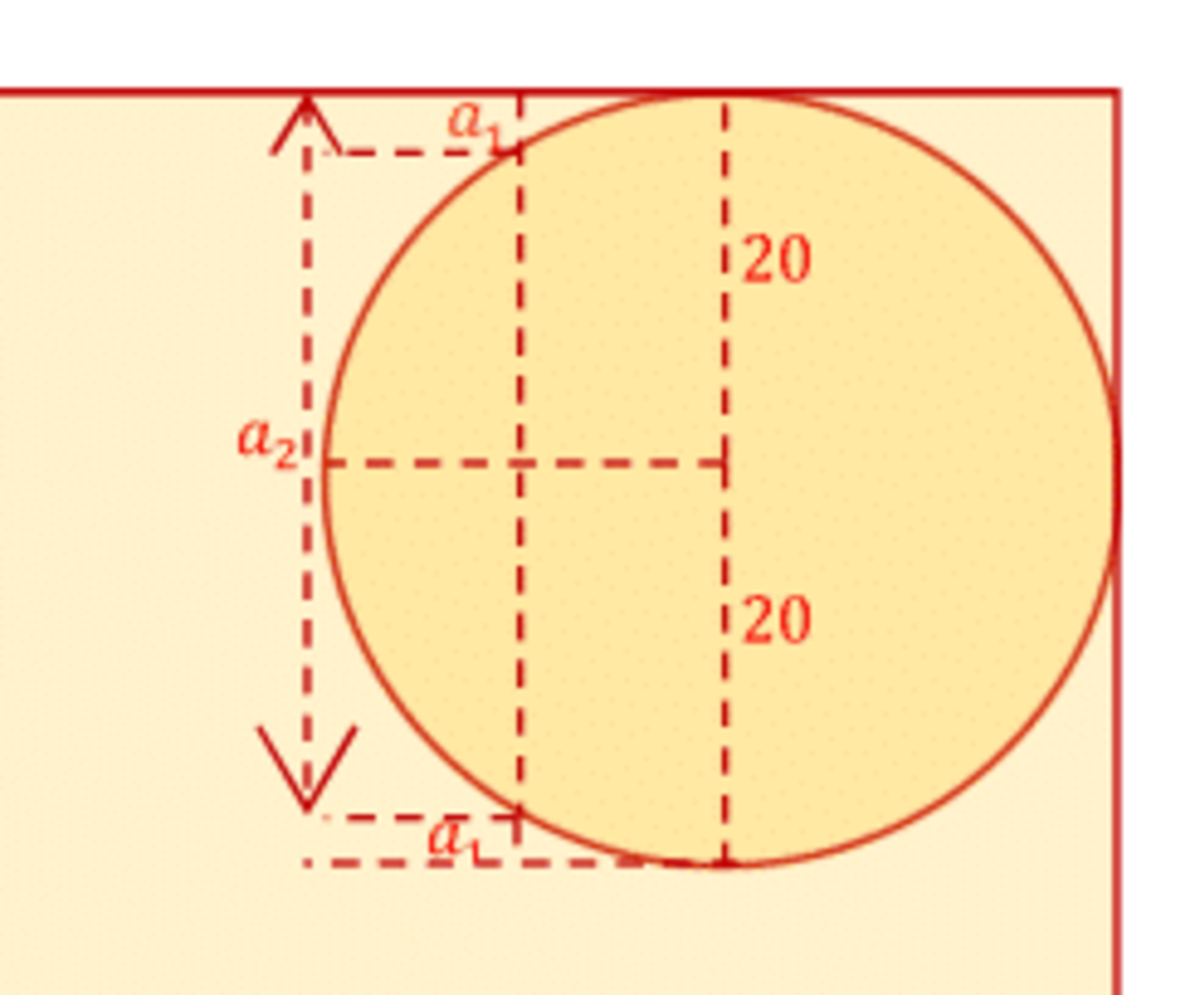
Distance a 2 + a 1 = 2 × 2 0 = 4 0
Note: unfortunately the software will not let me post my solution as a solution. So it's just a comment.
Log in to reply
what? a 2 + a 1 = 4 0 ? proof please . .
Log in to reply
You have a 2 = 2 x + a 1 . So I just continued to the other side and ended up with, starting from the wall a 1 , x , x , a 1 . The first a 1 + x = 2 0 , as you pointed out. The second x + a 1 = 2 0 . Total 2 0 + 2 0 = 4 0 .
Relevant wiki: Pythagorean Theorem
The above figure is not drawn to scale.
By Pythagorean Theorem
x = 2 0 2 − 1 0 2 = 3 0 0
Solving for a 2 , we have
a 2 = 2 0 + x = 2 0 + 3 0 0
Solving for a 1 , we have
a 1 = 2 0 − x = 2 0 − 3 0 0
Finally,
a 1 + a 2 = 2 0 − 3 0 0 + 2 0 + 3 0 0 = 4 0 f e e t