(Corrected!) It's Triangles All the Way Down
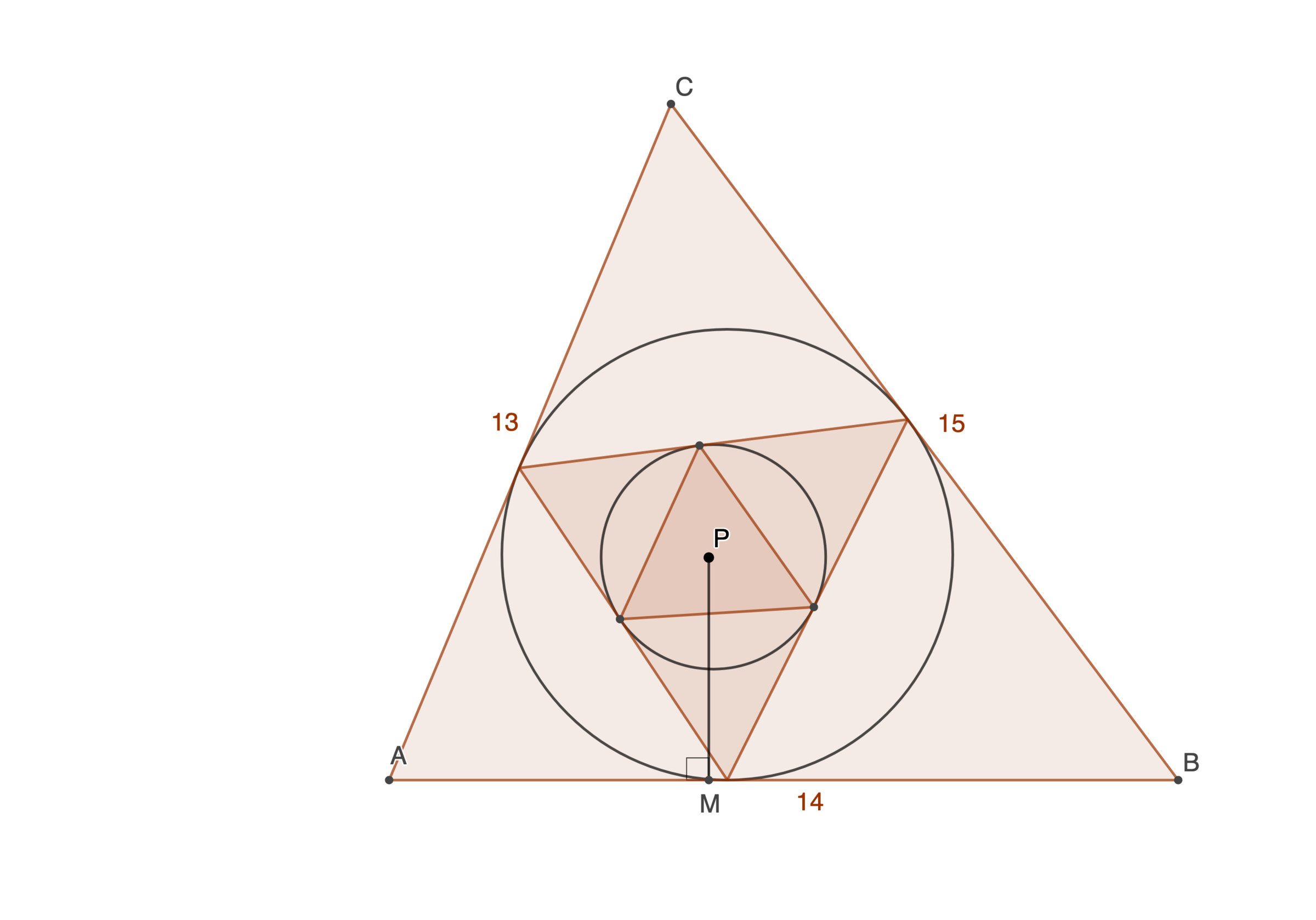
What happens to a triangle when one constructs its incircle , then it's contact triangle , followed by another incircle, and so on? It eventually converges to a point. Find that point, , for the 13-14-15 triangle shown in the figure, and submit the length of as
Extra Credit: I would love to find an analytical solution for the general problem. However, I don't know how to do that, and I have asked for help here if you care to take a look.
The answer is 39498.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Explanation
Let's solve it using complex number geometry.
Now, let the coordinates of triangle be z 1 , z 2 , z 3 and the side lengths be a , b , c and semi-perimeter be s
Now, let coordinates of contact triangle be z 1 ′ , z 2 ′ , z 3 ′
Now, z 1 ′ divides side joining z 2 and z 3 in ratio s − b : s − c .
So,
z 1 ′ = 2 s − b − c z 2 ( s − c ) + z 3 ( s − b )
Similarly
z 2 ′ = 2 s − a − c z 1 ( s − c ) + z 3 ( s − a )
z 3 ′ = 2 s − a − b z 2 ( s − a ) + z 1 ( s − b )
So, now we have recurrence relation between coordinates of triangle and coordinates of contact triangle, let us write the code to find the coordinates of the points of triangle when all three vertices coincide
For above question, we have z 1 = 0 + 0 i , z 2 = 1 4 + 0 i , z 3 = 5 + 1 2 i
Code
Output
Answer
So, P = 5 . 6 7 1 5 3 + 3 . 9 4 9 8 0 i , P M = Im ( P ) = 3 . 9 4 9 8 0
⌊ 1 0 4 × P M ⌋ = 3 9 4 9 8