Its Young's (excluded) not Old's (included)
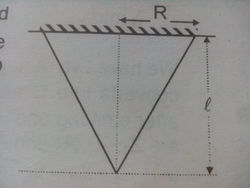 A cone of circular cross section having base radius
and height
and mass
is suspended from its base as shown in the figure. The material of the cone has young modulus
. The acceleration due to gravity is
. The elastic potential energy stored in the cone is
A cone of circular cross section having base radius
and height
and mass
is suspended from its base as shown in the figure. The material of the cone has young modulus
. The acceleration due to gravity is
. The elastic potential energy stored in the cone is
Find
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We take an elemental disk at a distance x from the bottom of thickness d x .
Radius of disk is given by r = L x R .
So weight of the cone below the disk = m g 3 1 π R 2 L 3 1 π ( L 2 x 2 R 2 ) x = L 3 m g x 3
Strain= A Y W e i g h t = Y π R 2 L m g x , A = A r e a o f d i s k = L 2 π x 2 R 2
Let the total elastic potential energy be E
d E = 2 1 Y ( S t r a i n ) 2 d V V = v o l u m e
d V = L 2 π x 2 R 2 d x
Putting the values we have d E = 2 π Y R 2 L 4 m 2 g 2 x 4 d x
E = 2 π Y R 2 L 4 m 2 g 2 ∫ 0 l x 4 d x = 1 0 π R 2 Y m 2 g 2 L
So we have a = 2 , b = 2 , c = 1 , d = 1 0 , e = 1 , f = 2
Hence a + b + c + d + e + f = 1 8