I've seen it before - 3
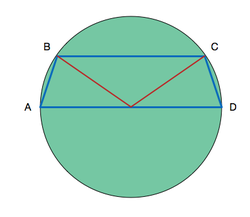 If
A
B
C
D
is an isosceles trapezium inscribed in a semi-circle with diameter
A
D
and
A
B
=
C
D
=
2
cm
and the radius of the semi-circle is
4
cm
, then the length of
B
C
(in cm) is:
If
A
B
C
D
is an isosceles trapezium inscribed in a semi-circle with diameter
A
D
and
A
B
=
C
D
=
2
cm
and the radius of the semi-circle is
4
cm
, then the length of
B
C
(in cm) is:
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
AC ^2= 8x+ + 4 . (Ptolomeu) ACD is a pitagorean AC^2 + 2^2= 64 Than, x=7
Extend hhe lines AB,DC so that we get an isosceles triangle with top P. Then the triangle OCD is similar to ADP, and it follows that AP=16, hence BP=14. The triangle PBC is similar to ADP, so that 14/16=BC/8 => BC=7.
Let the intersection of the red lines (as shown) be T. Then AT = BT = 4 (radii of circle). Now note that A B A T = 2 (#1). Next, extend AB and CD until they meet at point P. This means that: ∠ B A D = a ⟹ ∠ B C D = 1 8 0 − a ⟹ ∠ B C P = a = ∠ C B P Triangles ABT, BCP and ADP are similar so CP = BP = 2 x from (#1). Finally: D A D P = C B C P ⟹ 2 x + 1 = 4 ∴ x = 7
Δ A D C is right triangle. Applying Pythagoras' theorem, A C 2 = A D 2 − C D 2 = 8 2 − 2 2 = 6 0
Now applying Ptolemy's Theorem,
A D × B C + A B × C D = A C × B D
⇒ 8 × C D + 2 × 2 = A C × A C = 6 0
⇒ C D = 7
let h be the height of the trapezium.In triangle ABO,(2/4) * sqrt(4 * 4^2-2^2)=(1/2) * h * 4 or h=(sqrt 15)/2.Triangle BOC is an isosceles triangle,where the h will be the median of the triangle,applying pythagorean theorem we get BC/2=sqrt[4^2-{(sqrt 15)/2}^2] or BC/2=7/2 or BC=7
Draw CH is perpendicular to AD, O is the center of the semi-circle. Call K is the center of CD. ∠ H C D = ∠ K O D ⇒ O D C K = C D H D ⇒ D H = 2 1 B C = A D − 2 × D H = 8 − 1 = 7