I've seen it before - 6
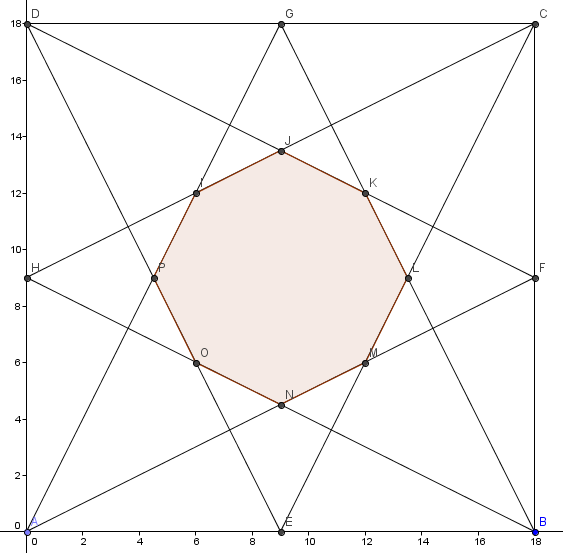 If
A
B
C
D
is a square with side
1
8
cm
and
E
,
F
,
G
,
H
are the midpoints of
A
B
,
B
C
,
C
D
,
D
A
repectively, then join
A
to
G
and
F
,
B
to
G
and
H
,
C
to
H
and
E
,
D
to
E
and
F
. An octagon is formed from the intersection of these lines, then the area of the octagon (the shaded region in the figure) is
If
A
B
C
D
is a square with side
1
8
cm
and
E
,
F
,
G
,
H
are the midpoints of
A
B
,
B
C
,
C
D
,
D
A
repectively, then join
A
to
G
and
F
,
B
to
G
and
H
,
C
to
H
and
E
,
D
to
E
and
F
. An octagon is formed from the intersection of these lines, then the area of the octagon (the shaded region in the figure) is
Note :-
-
The Octagon may or may not be a regular .
-
You can find more such problems here
Image Credit Aditya Raut
The answer is 54.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Uses coordinate geometry.
Set A to be the origin.
We can prove that the octagon is regular (will leave it to the reader)
Also, we know that the center of the octagon is the center of the square. (Again, up to the reader to prove) Thus, its center is ( 9 , 9 ) .
Take any vertex of the octagon. So let's say it's the bottom one (Point M I think). The coordinates of the point is simply the intersection between the line that passes through A and the midpoint of C D . Knowing that the side length of the square is 18, we then know that D = ( 1 8 , 0 ) . Solving this, we have the equations y = 2 1 x and y = − 2 1 x + 9 . Therefore their intersection point, and one of the octagon's vertices, is ( 9 , 2 9 ) Doing the same thing to any the next vertex (counter-clockwise), we have it's coordinates being ( 1 2 , 6 ) . We can now compute for the triangle's area. Which is conveniently 8 1 of the octagon's area.
We can now calculate the triangle's area. Its area is then 2 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 9 9 1 2 9 9 2 9 6 9 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ = 2 1 ∣ ( 2 8 1 + 5 1 + 1 0 8 ) − ( 8 1 + 5 4 + 5 4 ) ∣ = 4 2 7 .
Thus, the area of the rectangle is 4 2 7 × 8 = 5 4 .
Did u try generalization?
Actually the octagon is not regular, although this doesn't affect your solution as you only made use of symmetry. Nice and short solution though :)
I did almost the same way. First i determined the vertices and then put all the vertices in Shoelace Metrix. (According to Wikipedia : Shoelace formula)
I got a little different solution.
Also, let A = ( 0 , 0 ) . Since the octagon is regular, it's sufficent to find one side. Let's find the side M N . To do so, we'll find the equation of the lines A F and B H . They are y = 2 x and y = − 2 x + 9 , respectively. And their intersection point is N = ( 9 , 2 9 ) .
Now, do the same with the lines A F and C E . They are y = 2 x and y = 2 x − 1 8 , respectively. Their intersection point is M = ( 1 2 , 6 ) .
Finally, calculate the side M N with the distance formula: M N = ( 1 2 − 9 ) 2 + ( 6 − 2 9 ) 2 = 9 + 4 9 = 2 3 5 .
Use the formula of the area of the octagon:
A r e a = 2 ( 2 + 1 ) L 2 = 2 ( 2 + 1 ) 4 4 5 = 2 4 5 + 4 5 2 ≈ 5 4 . 3 1 , which is very near from 54. Is my approach correct?
The horrifying fact: the octagon in the middle is not regular...
Actually the octagon is not regular(u can check it by finding any 2 consecutive angles)
So DHZG is also a 9X9 square, 4 1 of ABCD, with P and J midpoints of the respective sides.
∴ H P = P Z = 2 9 . With X on GP draw JX || PZ,........... with Y on GZ draw IY || PZ, with Q on PZ draw XQ ⊥ P Z , R = X Q ∩ I Y . a l l o n s k e t c h . Δ G P Z , J i s m i d p o i n t o f G Z , ∴ X J = 2 P Z = 4 9 . H Z ⊥ X Q a n d G Z ∴ X Q ∣ ∣ J Z a n d X J ∣ ∣ Q Z ∣ ∣ R Y ∴ R Y = X J = 4 9 . S i n c e X P ∩ J H a n d X J ∣ ∣ H P , Δ I J X Δ I H P , ∴ I P X I = H P X J = 2 1 . B u t i n Δ X P Q , I R ∣ ∣ P Q ⟹ P Q I R = a + 2 a a , ∴ I R = 3 4 9 = 4 3 . ∴ h e i g h t o f Δ I Z J I Y = I R + R Y = 3 . ∴ A r e a o f Δ J I Z = 2 1 + J Z ∗ I Y = 4 2 7 . B u t ∵ o f s y m m e t r y , A r e a o f o c t a g o n = 8 t i m e s Δ J I Z . A r e a o f o c t a g o n = 5 4
In spite of symmetry, adjacent angles of the octagon are not equal, only alternative angles are equal.