Jackson Style
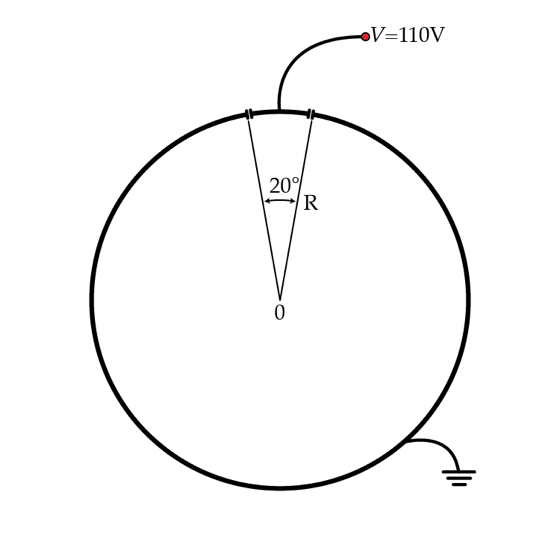
Consider a very long hollow metallic cylinder of radius
R
. A section of the cylinder (corresponding to
θ
=
2
0
∘
) is kept at constant potential
V
=
1
1
0
V
while the rest of the cylinder is kept at
0
V
(grounded) as shown in the figure. Find the potential
V
a
x
i
s
in Volts
on the axis of the cylinder (point O).
The answer is 6.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
We called this challenge "Jackson Style" because of Jackson's book on Classical Electrodynamics where one finds similar problems. These type of problems require, in general, advanced mathematics. However, our problem can be easily solved by noticing that 2 0 × 1 8 = 3 6 0 . What we have in mind is the following: One can take 18 copies of this cylinder and superpose them to obtain one cylinder kept, entirely, at constant potential V = 1 1 0 V . Clearly, for such cylinder the potential at the center (and everywhere inside the cylinder) will be 1 1 0 V . By symmetry, the contribution to the potential on the axis coming from each of the 18 cylinders is equal and we have that 1 8 V a x i s = 1 1 0 V → V a x i s = 1 8 1 1 0 = 6 . 1 V which gives us the sought potential.
I didnt understand how the potential could be different for surface of the same conductor. Electric field has to be zero within the conductor so potential difference cannot exist within the conductor ?
The Potential at Point O = Potential Difference between the minor arc and the grounded arc * area enclosed by the minor arc/total area,
Hence the potential at point O = ( 1 1 0 V − 0 V ) × 3 6 0 2 0 = 6 . 1 1 V
By Maxwell's equations, we have ∇ ⋅ E = ϵ 0 ρ = 0 , because there is no charge inside the cylinder.
The voltage satisfies E = − ∇ V . So, ∇ 2 V = ∇ ⋅ ∇ V = − ∇ ⋅ E = 0 .
This is Laplace's Equation. By symmetry, V is constant along any line parallel to the axis of the cylinder. Thus, ∇ 2 V = 0 holds on any planar cross-section perpendicular to the axis of the cylinder. A property of solutions to Laplace's Equation in a plane is that the value at a point is equal to the average value around any circle centered at that point.
Thus, V a x i s is simply the average voltage on the boundary of the cyllinder which is 3 6 0 ∘ 2 0 ∘ ⋅ 1 1 0 V = 6 . 1 1 V .