Japanese Mathematical Olympiad 1994

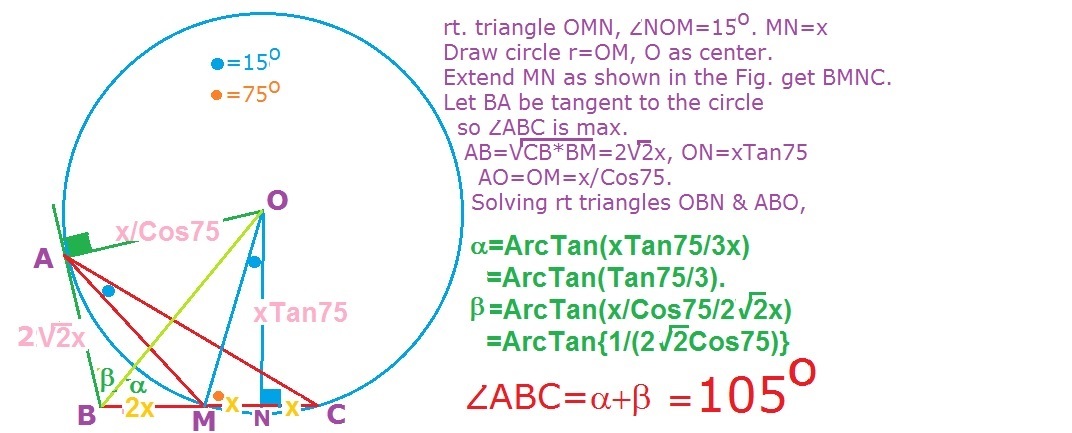
Consider this diagram on the left.

If $\angle COM=30^{\circ},$ then $A$ would be on the circle.

Let $C(1,~0)$ and you see that $M \left(\dfrac{\sqrt{3}}{2},~\dfrac{1}{2}\right).$

Therefore $B \left(\sqrt{3}-1,~1\right).$

.

.

.

.

Since we are maximizing $\angle ABC,$ the maximum would be reached when $\overline{AB}$ is tangent to the circle.

Note that the $y$ -coordinate of $B$ is $1$ and therefore the tangential line would be perpendicular to the $y$ -axis, and that $\angle OCB=75^{\circ}.$

$\therefore$ The maximum of $\angle ABC$ is $180^{\circ}-75^{\circ}=\boxed{105^{\circ}}.$