Japanese Mathematical Olympiad 2005 (Revised)

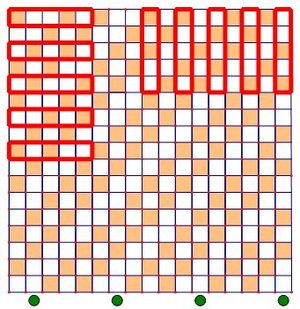
Consider 115 red coins: In each step (horizontal, vertical, diagonal) exactly 2 of them will be flipped! Because of the parity it is not possible to have all (red) coins showing tails.

Consider the $17\times17$ array of coins, and look at the special set of coins I have coloured orange. There are $7$ such coins in each column, except for the $4$ columns marked with a green dot, which have $6$ such coins, and hence there are $7\times13 + 6\times4=115$ orange coins altogether - an odd number. As the ten red rectangles show, any $5\times1$ rectangle covers precisely two orange coins. Thus any legal move reverses the state of two orange coins, and hence the parity (evenness/oddness) of the number of orange coins that are showing Heads remains constant. Since there are an odd number of orange coins, there will always be an odd number of orange coins that show heads at any future time. If all the coins showed tails, then in particular all the orange coins would show tails, and hence there would be an even number of orange coins showing heads. This is impossible. Thus it is not possible to have all coins showing tails.