JEE-2015
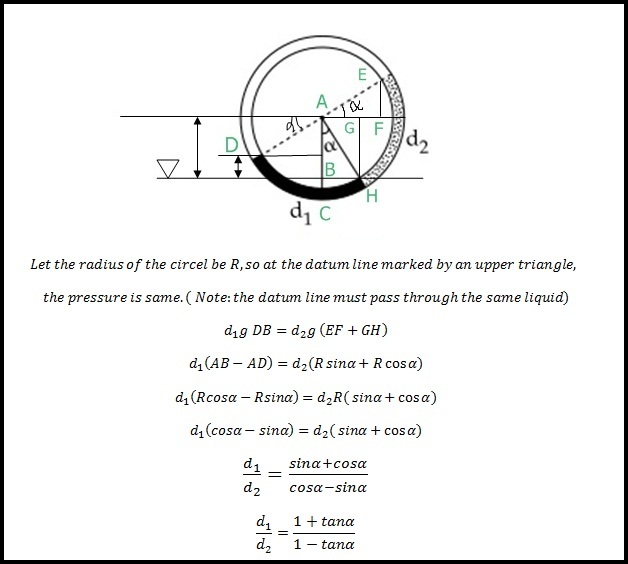
 There is a circular tube in a vertical plane. Two liquids which do not mix and of densities
d
1
and
d
2
are filled in the tube. Each liquid subtends
9
0
∘
angle at centre. Radius joining their interface makes an angle
α
with vertical. Ratio
d
2
d
1
is:
There is a circular tube in a vertical plane. Two liquids which do not mix and of densities
d
1
and
d
2
are filled in the tube. Each liquid subtends
9
0
∘
angle at centre. Radius joining their interface makes an angle
α
with vertical. Ratio
d
2
d
1
is:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I've heard of the "JEE style" many a times here on Brilliant, and so I figure I might as well use it.
If d 1 = 0 , then clearly α = − 4 π . Since the only option that matches d 2 d 1 = 0 is 1 − tan α 1 + tan α , that must be the right answer.
Useful, thanks !
Hey there, sorry for a dumb doubt but how did you decide alpha's value when d_1 = 0?