Rational Function

Another interesting solution can be derived using a bit of intuition and geometry.

Let $p_1(x) = x^2+ax+b,$ and let $p_2(x) = x^2+2x+3$ which is always positive. Then, our inequality from the range is equivalent to $-5p_2(x) \le p_1(x) \le 4p_2(x).$

Now, let's approach this geometrically. If we think about this graphically, we have two parabolas with the same $x$ -coordinate vertex, and a third parabola which is always between them.

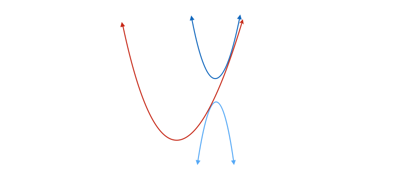
This red parabola, $p_1(x),$ must equal each other parabola once since the range is $[-5,4]$ not $(-5,4).$ This single intersection (tangency) is equivalent to saying that there is a double-root for each of the equations $-5p_2(x) = p_1(x)$ and $4p_2(x)=p_1(x).$

Note that $\alpha x^2 + \beta x + \gamma = 0$ has a double root if and only if $\left(\frac{\beta}{2\alpha}\right)^2 = \frac{\gamma}{\alpha},$ since that allows it to be factored as $\alpha \left( x - \frac{\beta}{2\alpha}\right)^2=0.$ If this is unfamiliar, check out Completing The Square .

Now, $-5p_2(x) = p_1(x) \ \iff \ 6x^2 + (10+a)x + (15+b) = 0,$ so we get our double root when $\left(\frac{10+a}{12}\right)^2 = \frac{15+b}{6} \ \iff \ \boxed{(10+a)^2 = 24(15+b)}.$ Similarly, $4p_2(x) = p_1(x) \ \iff \ 3x^2 + (8-a)x + (12-b) = 0,$ so we get our double root when $\left(\frac{8-a}{6}\right)^2 = \frac{12-b}{3} \ \iff \ \boxed{(8-a)^2 = 12(12-b)}.$

Solving these two equations simultaneously, we find $(a,b)$ as $(14,9)$ or $(-10,-15).$ Since $a$ and $b$ are positive integers, we have $(a,b) = (14,9).$ Thus, $a^2+b^2-ab = 14^2 + 9^2 - 14\cdot 9 = \boxed{151}.$