JEE-Advanced 2014 (1/40)

Is all about roots, so I took $f(x)=0$ . This means $x^{5}=5x-a$ , that, by graph, has an interval of $a$ with 3 solutions, for $a∈[-4,4]$ , because $y=5x-a$ is tangent for $a=-4$ or $a=4$ . If $a$ is out of $[-4,4]$ it has only one solution.

Let a function be given by $g(x) = x^5 - 5x$ .

When you factorize $g(x)$ , you get: $g(x) = x(x^2 + \sqrt {5})(x+ \sqrt {\sqrt {5}})(x - \sqrt {\sqrt {5}})$

Hence one can assume from this that $g(x)$ has 3 real roots, as $x^2 + \sqrt {5} = 0$ has no real roots. The 3 real roots being $0, \sqrt {\sqrt {5}}$ and $-\sqrt {\sqrt {5}}$ .

The maximum and minimum values of $g(x)$ can be found:

$g'(x) = 5x^4 - 5 = 5(x^2 + 1)(x - 1) (x + 1) = 0$

$x = 1, -1$

$g(x) = 1^5 - 5(1) = -4$ <-- minimum value of $g(x)$

$g(x) = (-1)^5 - 5(-1) = 4$ <-- maximum value of $g(x)$

Since the coefficient of $x^5$ (and taking note that $5$ is an odd number) in $g(x)$ is positive, and since $g(x)$ has 3 real roots, one can imagine $g(x)$ to be similar to this image shown:

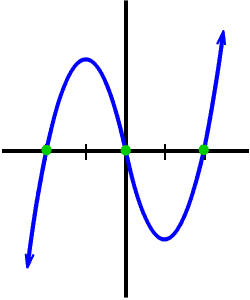
$f(x)$ is similar to $g(x)$ , but it is displaced upward or downward (parallel to the y-axis), depending on the value of the constant $a$ .

One can determine that $f(x)$ would still have three real roots unless $|a|>4$ , and in that case, $f(x)$ would only have one real root.

Hence the answer is $\boxed {(B) and (D)}$ .

Hint: Use Intermediate Value Theroem.

Hint: consider g(x)=x^5-5x and plot its graph and then work with options.