JEE Advanced Calculus problem
Determine f ( x ) = a x 2 + b x + c , where a > 0 , whose roots are ϕ 1 and ϕ 2 where 0 < ϕ 2 < ϕ 1
If, for some real value α < β where α + β = 5 , ∫ 0 α f ( x ) d x = 0 and ∫ 0 ϕ 1 f ( x ) d x + ∫ ϕ 2 β f ( x ) d x = ∣ ∫ ϕ 1 ϕ 2 f ( x ) d x ∣ The value of x such that f ( x ) is minimum can be written in the form of q p , where p and q are coprime. Find p + q
Original Question
 -Also note that alpha is less than beta.
-Also note that alpha is less than beta.
-
The answer will be in form of q p .
-
Find p+q.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
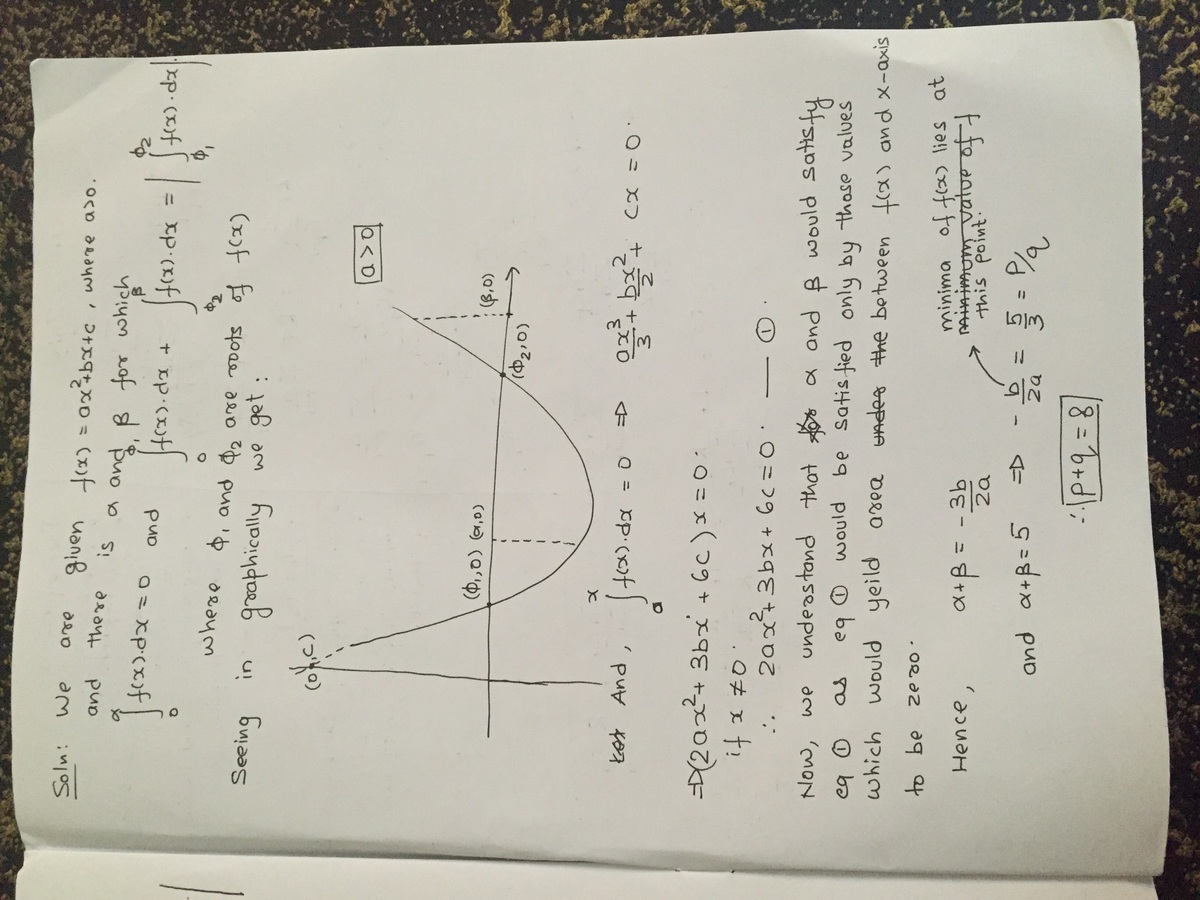
You said phi1 > phi2 And then i wonder how come it reached level 5.
i am getting -5/3 thats why i am getting -2this is because phi2<phi1 thats why the modulus will be opened as negative
i was such an idiot. i got the answer. i have to submit p+q. i submitted p/q. then i saw a message the answer is integer. then i thought i was wrong.very sad.
The question says phi1>phi2, but the solution says phi1<phi2. It makes a difference.
Log in to reply
Yeah I forgot about the order of them now that I rechecked it seems weird
If it was otherwise I think there will be a contradiction and we will get a negative number for the absolute value