JEE Advanced Electrostatics (Non-conductors) 1

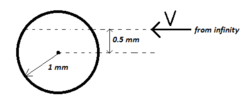
The particle would just graze past the sphere at the mentioned point in a direction tangential to the sphere at that point, as shown in the following diagram.

First of all, we need to conserve angular momentum about a point, let's say about the center of the sphere. Conserving angular momentum, we get

$\begin{aligned} & L_{i} = mvr\sin{\left(\dfrac{5\pi}{6} \right)} &&& \cdots(1) \\ & L_{f}=m(v')r\sin{\left(\dfrac{\pi}{2}\right)} &&& \cdots(2) \end{aligned}$

Equating (1) and (2), we get

$\begin{aligned} & L_{i}= L_{f} \\ & mvr\sin{\left(\dfrac{5\pi}{6}\right)} = m(v')r\sin{\left(\dfrac{\pi}{2}\right)} \\ & \boxed{\dfrac{v}{2}=(v')}\end{aligned}$

Now using the principle of conservation of energy we get

$\begin{aligned} & \dfrac{1}{2}mv^{2}- \dfrac{1}{2}m\left(\dfrac{v}{2} \right)^{2}=\dfrac{1}{4\pi \epsilon_{0}}\dfrac{Q^2}{r} && \left( Q= \dfrac{1}{3} \mu \text{C} \text{ and } m=1 \text{kg} \right) \\ & v= \sqrt{ \dfrac{8Q^2}{3 \times4 \pi \epsilon_{0}mr}} \text{ms}^{-1} \\ & v= \dfrac{8\times 9 \times 10^9 \times 10^3}{3 \times 9\times 10^{12}} \text{ms}^{-1} \\ & v= \sqrt{\dfrac{8}{3}} \text{ms}^{-1}=\boxed{1.632 \text{ms}^{-1}} \end{aligned}$

This would be trajectory.

Write equation for energy conservation and angular momentum conservation. .. If the mass is 'm' charge is 'q' radius is 'r' then minimum speed 'v' $=q\times\sqrt{\dfrac{8k}{3mr}}$ Where $k$ has d usual meaning