JEE Advanced Mechanics (Equilibrium) 1
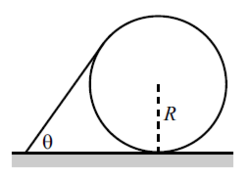 A stick rests on a circle of radius
. The stick makes an angle
with the horizontal and is tangent to the circle at its upper end. Calculate
for which stick is most likely to slip on ground. Enter answer as
where
is in degrees.
A stick rests on a circle of radius
. The stick makes an angle
with the horizontal and is tangent to the circle at its upper end. Calculate
for which stick is most likely to slip on ground. Enter answer as
where
is in degrees.
Details and Assumptions
-
Friction exists at all points of contact.
-
Assume that stick is large enough to keep the system at rest.
This problem is a part of My picks for JEE Advanced 1
The answer is 4294.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Above, the blue forces are the ones acting on the stick, while the red ones are the ones acting on the circle (forces not to scale). Note the importance of the direction of the friction forces F 1 , F 2 and F 3 acting on each object and the use of Newton's third law to denote N 2 (the normal force due to contact between objects) and F 2 .
My opinion is that drawing those forces correctly is the most important step of the problem, what's next is mostly maths. We can now write Newton's second law in various equations as follows:
Eq. 1: F 1 + F 2 cos θ − N 2 sin θ = 0
Eq. 2: N 1 + N 2 cos θ + F 2 sin θ − m g = 0
Eq. 3: N 2 sin θ − F 2 cos θ − F 3 = 0
Eq. 4: m g 2 L cos θ − N 2 L = 0
Eq. 5: F 2 R − F 3 R = 0
Note Eq. 1 and 2 are the sum of forces in the horizontal and vertical direction on the stick, Eq. 3 is the sum of forces in the horizontal direction on the circle, Eq. 4 is the sum of torques on the stick with respect to an axis perpendicular to the plane in the lower end of the stick ( L is the length of the stick), and Eq. 5 is the sum of torques on the circle with respect to an axis perpendicular to the plane on the center of the circle. All of the sums equaling to 0 state equilibrium.
Eq. 5 and 4 give, respectively,
Eq. 6: F 3 = F 2
Eq. 7: N 2 = 2 m g cos θ
Replacing Eq. 6 and 7 on Eq. 3 we get
Eq. 8: F 2 = 2 ( 1 + cos θ ) m g sin θ cos θ
Replacing Eq. 7 and 8 on Eq. 1 and 2 we get, respectively,
Eq. 9: F 1 = 2 ( 1 + cos θ ) sin θ cos θ m g
Eq. 10: N 1 = ( 1 − 2 cos θ ) m g
So far we haven't made any assumption except that the system is in equilibrium. Here's the next one: if the stick is about to slip on the ground, we can safely affirm that the friction force is equal to the normal force applied on that point times some coefficient, say μ . This way we can safely combine Eq. 9 and 10 to obtain
Eq. 11: μ = 2 + cos θ − cos 2 θ sin θ cos θ
When we plot μ vs. θ , we get something like this
We can see there is a value of θ for which μ is maximum. We have chosen our assumption so that the stick slips on ground. So if we choose the maximum value of μ possible and it still slips, it means that the value of θ for which μ is maximum is the one for which stick is most likely to slip on ground. To do so we derivate and find that this value is such that
cos θ = 3 − 1
or simply θ = 4 2 . 9 4 . Thus, the answer is ⌊ 1 0 0 θ ⌋ = 4 2 9 4