JEE Advanced Mechanics (Equilibrium) 2
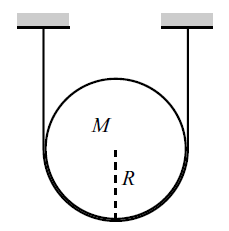 A disk of mass
M
and radius
R
is held up by a massless string, as shown in Figure. The surface of the disk is frictionless. What is the normal force per unit length the string applies to the disk?
A disk of mass
M
and radius
R
is held up by a massless string, as shown in Figure. The surface of the disk is frictionless. What is the normal force per unit length the string applies to the disk?
This problem is a part of My picks for JEE Advanced 1
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Keshav Tiwari Done!
Thanks a lot. Got it !
Why exactly is T=Mg/2 ?? And thank you
Log in to reply
Balancing forces in vertical gives that.
How did you get the sum as 2 T sin 2 d θ ? One is T and the other is T sin 2 d θ , so how does the sum become the one you mentioned?
Also, can you please also explain in a little deeper that why will they not be equal?
The question says per unit arc length that must b N/(pi)R right?
the integral of Ncos(x)dx = dmg from 0 to pi. so the result,2N=Mg N=MG/2
Normal Force per unit=N/R so,MG/2R
I did not understand your solution. How is normal force per unit N/R ?
What about the tension? Can we neglect that?
Can you please post a better solution ? @Pranjal Jain
Consider the normal force, N d θ , on a small arc of the disk that subtends and angle d θ . The tension forces on each end of the corresponding small piece of string almost cancel, but they don’t exactly, because they point in slightly different directions. Their non-zero sum is what produces the normal force on the disk. From figure, we see that the two forces have a sum of 2 T sin 2 d θ , directed inward. Since d θ is small, we can use sin x = x to approximate this as T d θ . Therefore, N d θ = T d θ , and so N = T . The normal force per unit arc length, R N , then equals R T . Using T = 2 M g , we arrive at R N = 2 R M g .