JEE Coordinate (2)!

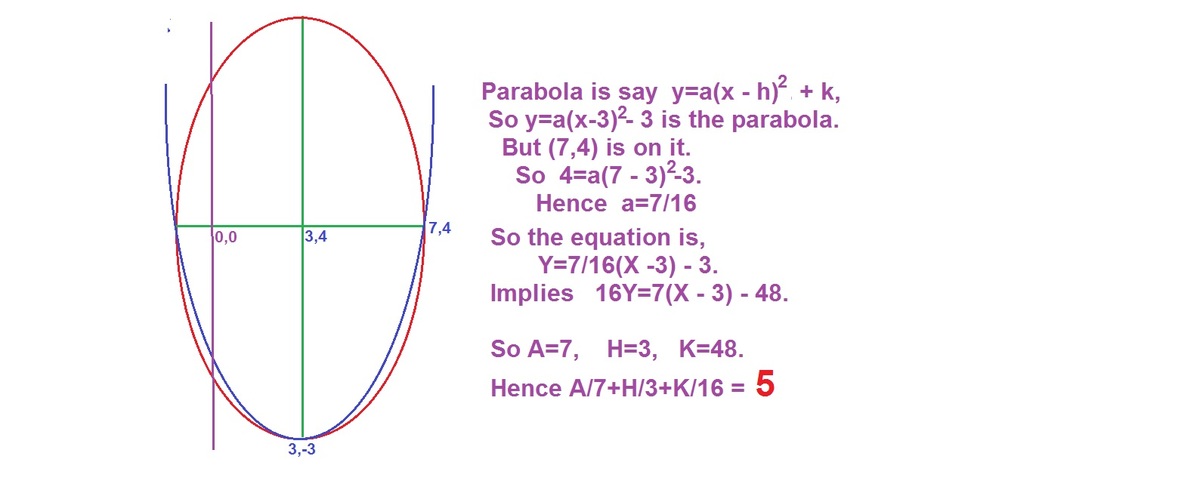
Given the equation of an ellipse is

$\frac{(x-3)^2}{16} + \frac{(y-4)^2}{49} = 1 .$

A parabola is plotted such that its vertex is the lowest point of the ellipse, and it passes through the ends of the minor axis of the ellipse above. If the equation of the parabola is in the form

$16y = A(x-H)^2 -K,$

where $A,H,K$ are all constants. Find $\dfrac A7 + \dfrac H3 + \dfrac K{16}$ .

# This is a part of my set Practice for JEE 2017!