JEE Main 2016 (12)

$\text{Let P(Xq,Yq). Q(Xq,Yq). So from midpoint formula }\\ \color{#3D99F6}{ ~ Xp+Xq=16,} \text{ and Yp+Yq=12, that is } \dfrac { 15} 8*Xp+\dfrac 3 {10}*Xq=12.\\ So~~ - 12Xp -12Xq= -192,~ and~~\color{#3D99F6}{ 75Xp+12Xq=480, }~ gives~ 63Xp=288. \implies ~Xp=\dfrac{32} 7.\\ \therefore~ Yp=\dfrac{32} 7*\dfrac{15} 8=\dfrac{60} 7.\\ PQ=2*\{(Xp,Yp)~~ to ~~(8,6)\}\\ \therefore~~ PQ=2*\sqrt{\left (8- \dfrac{32}{7} \right )^{\Large 2}+ \left (6- \dfrac{60} 7 \right )^{\Large 2} } =\dfrac{12} 7\sqrt{4^2+3^2}= \dfrac{60} 7=\dfrac m n.\\ m - 8n=60- 56=4.$

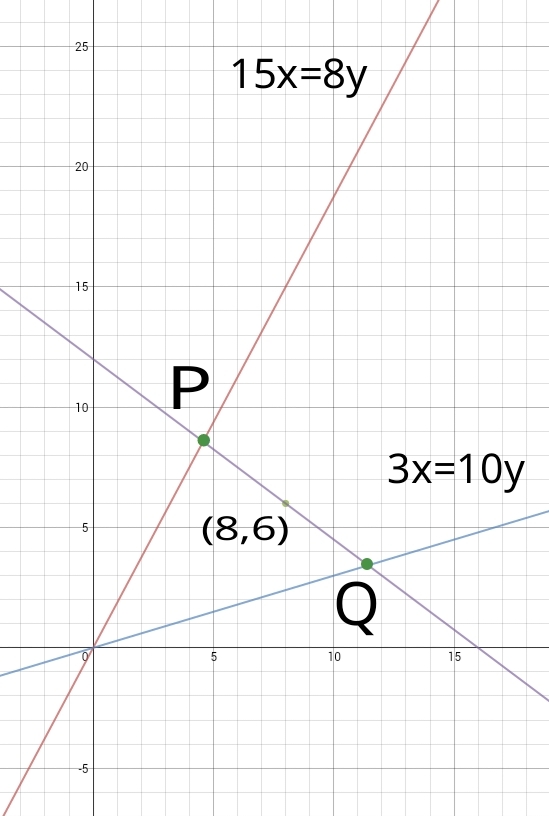
Let,

$P=(x_1,y_1)$ and $Q=(x_2,y_2)$ .

According to mid point formula (corollary of section formula ),

$\frac{x_1+x_2}{2}=8$ ... ( $1$ ) and $\frac{y_1+y_2}{2}=6$ ... ( $2$ )

$x_1+x_2=16$ and $y_1+y_2=12$

Also, $15x_1=8y_1$ and $3x_2=10y_2$ .

Hence ( $2$ ) can be written as $\frac{15}{8}x_1+\frac{3}{10}x_2=12$ .

Solving ( $1$ ) and ( $2$ ),

We get $x_1=\frac{32}{7},x_2=\frac{80}{7},y_1=\frac{60}{7} \text{ and } y_2=\frac{24}{7}$ .

Applying distance formula,

$PQ=\sqrt{\left( \frac{32}{7}-\frac{60}{7}\right)^2+\left(\frac{80}{7}-\frac{24}{7}\right)^2}$

$PQ=\frac{60}{7} =\frac{m}{n}$

Now,

$m-8n=\boxed{4}$