JEE-Mains 2014 (8/30)

let s(n)= $10^9$ +2(11)( $10^8$ ) +....... then $\frac{11}{10}$ s(n)= (11)( $10^8$ ) + 2( $11^2$ )( $10^7$ )+ ..... by subtracting these two we get $\frac{-1}{10}$ s(n)= $10^9$ +(11)( $10^8$ ) + ( $11^2$ )( $10^7$ ) + ......... - $11^9$ (11) apply GP formula where a= $10^9$ , r= $\frac{11}{10}$ , n=10 and then find s(n). you will get s(n)=( $10^9$ )( $10^2$ )

divide by 10^9. You get k=(11/10)^0+2(11/10)^1+..........+10(11/10)^10 ...i i*11/10.....ii ii - i; we get k=100.

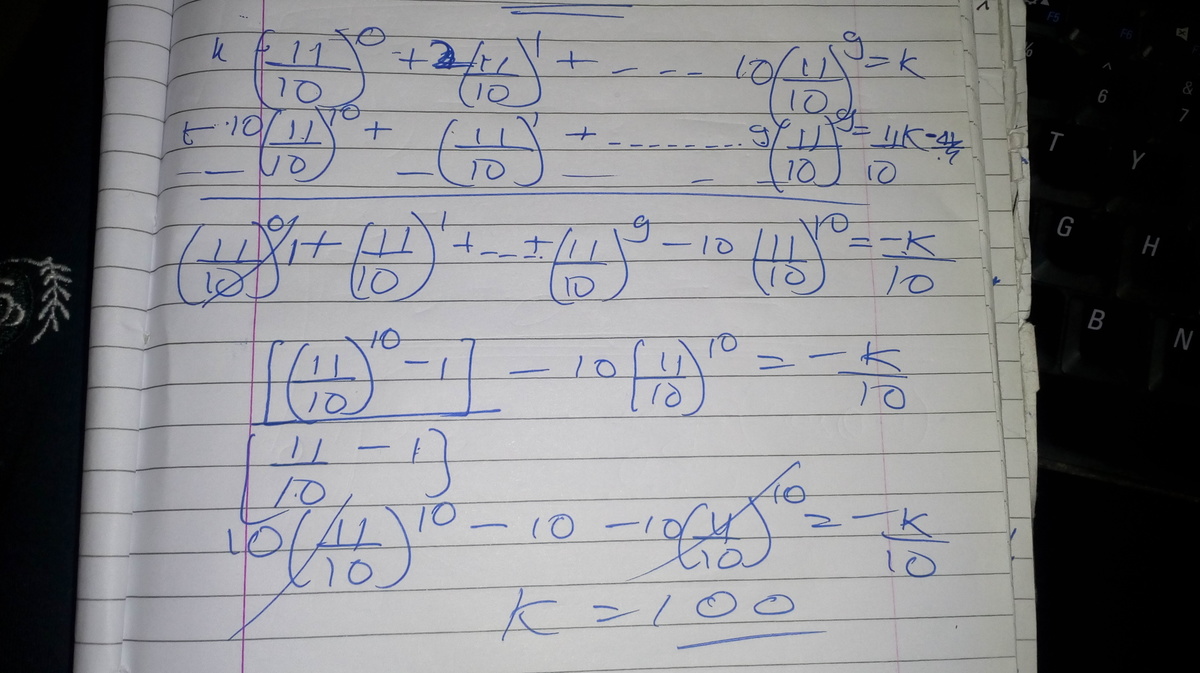Sorry not good handwriting :-)

Bad way!

Just helpful for elimination of options.

Assume $11$ to be $10$ for time being. And solve...We get that $k>55$ .

So $4.41$ and $12.1$ are obviously wrong options...

Since probability is $0.5$ of getting correct option, we can make a guess now.

$\displaystyle k=\sum_{n=1}^{10}n*1.1^{n-1}.~~~an~A\!-\!G~~progression.\\ ~~~~ \\ \therefore~~k=\dfrac{a-\{a+(n-1)*d\}r^n}{1-r} +\dfrac{d*r(1-r^{n-1}) }{1-r^2 }.\\ ~~\\ Our~a=d=1,~~r=1.1.\\ ~~~\\ Substituting~we~get~~\huge \color{#D61F06}{k = 100}.$