JEE Mains Mechanics (Equilibrium) 1
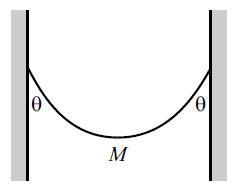 A chain of mass 2 Kg hangs between two walls, with its ends at the same height. The chain makes an angle of
θ
=
6
0
∘
with each wall, as shown in figure. Find the tension in the chain at the lowest point (mid-point).
(
g
=
9
.
8
S
I
u
n
i
t
s
)
A chain of mass 2 Kg hangs between two walls, with its ends at the same height. The chain makes an angle of
θ
=
6
0
∘
with each wall, as shown in figure. Find the tension in the chain at the lowest point (mid-point).
(
g
=
9
.
8
S
I
u
n
i
t
s
)
This problem is a part of My Picks for JEE Mains 1
The answer is 16.974.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nicely explained!
Very well explained!!
Let the mass of the string be m.
Visualize it like two blocks of mass m/2 attached together by a light in-extensible string and each of them attached to the wall by another strings .(total strings three).
Let the tension in the common string be T and other strings be t(tension will be same in other two strings ).
t s i n ( θ ) = T
t c o s ( θ ) = m g / 2
dividing both eq
we get
t
a
n
(
θ
)
=
2
T
/
(
m
g
)
so T= 2 ( m g t a n ( θ ) )
Substituting given values we find T=16.97 N
Note:This method cannot be executed if we have to calculate tension at any other point on string with these parameters only.
The force in the y-direction, Fy=0
The force in the x-direction, Fx= (m)(g)(sin theta) -T
T= (m)(g)(sin theta)
T= (2kg)(9.8 m/s^2)(sin 60)
T= 16.9N = 17N
The rope's weight is being supported at the two points of contact with the walls. The tension at these points is pulling on the walls, and thus by Newton's Third law there is an equal and opposite force by the wall on the rope. Given the symmetry of the problem we may infer that the tension is the same at both points of contact, and thus the load of 1 9 . 6 N must equally distributed over the vertical components of the two support forces. This means that each support force must be 1 9 . 6 N because cos 6 0 ∘ = 2 1 . A little trig will show that the horizontal component of either of the forces is 9 . 8 3 . These components are what give rise to the tension at the lowest point of the rope, seeing as it is also horizontal. Do not add the horizontal components. Two people pulling on a rope from opposite ends with the same force will give rise to the same tension as one person pulling with an identical force and the other end tied to a wall.