JEE Mains Mechanics (Equilibrium) 1
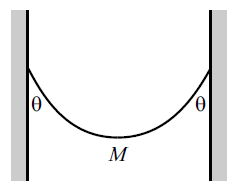 A chain of mass 2 Kg hangs between two walls, with its ends at the same height. The chain makes an angle of
θ
=
6
0
∘
with each wall, as shown in figure. Find the tension in the chain at the lowest point (mid-point).
(
g
=
9
.
8
S
I
u
n
i
t
s
)
A chain of mass 2 Kg hangs between two walls, with its ends at the same height. The chain makes an angle of
θ
=
6
0
∘
with each wall, as shown in figure. Find the tension in the chain at the lowest point (mid-point).
(
g
=
9
.
8
S
I
u
n
i
t
s
)
This problem is a part of My Picks for JEE Mains 1
The answer is 16.974.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
WHY would you start with the statement that T2 equals half mg divided by cos theta? Could you explain the logic of the first equation? Look at your diagram and state T1 will equal the horizontal component of the total tension in the rope which is half mg. Hence your final equation. Hence your first two equations. But how do you start with your fist two?
Doesn't the bottom also have vertical tension?
The tension in the string is going to be the same at all points in the string. The only thing that changes, are the vectors of the forces, producing the tension.
Log in to reply
This is clearly not true when the string has weight. In a long length of chain, hanging vertically, the bottom link has no tension, the one above it has the tension of one link, etc. The top has the tension of the whole chain.
"The tension in the string is going to be the same at all points in the string",it's only for mass-less strings not for a string having mass is unequally distributed!!!!
don't we consider normal forces from the wall?
Can u explain it further?
Can u explain it further
I think its even easier, u guys are making things complicate, at the bottom point, tension acting will be horizontal in opposite directions and mg downward, in free body diagram correct?
So tan(theta) = x/y = (T/2)÷mg
Sorry this is unintelligible to me
I think this is same solution I have
Take this challenge : The problem is same The angle is 60 degree only. The distance between the two wall is 12 m your are required to calculate the length of string. The string is inextensible Hint : parabola
It's a catenary, not a parabola, you know.
Log in to reply
The way I solved this was to say that the tension at the mid-point is equal to the horizontal force component at either end. The vertical force component at the ends is 2kg x 9.8 in total, so 1kg x 9.8 each end. I calculated the horizontal component by trigonometry: f h = f v tan θ
this solution is brilliant, thanks man
Thank you, the other explanations only worked if you already new the correct explanation
In the hanging chain, gravity and the reaction at the supports are the only forces involved. The vertical component at the support is W/2=(1)(9.8)N. Therefore, the tangential component in the chain is T=9.8/cos60=19.6N. The horizontal tension in the chain is constant throughout its length and is Tx=(T)sin60=19.6sin60=16.974N

Here is an easy situation because the tension is asked at the lowest point.So diagram is slightly modified(this can be done in this case.)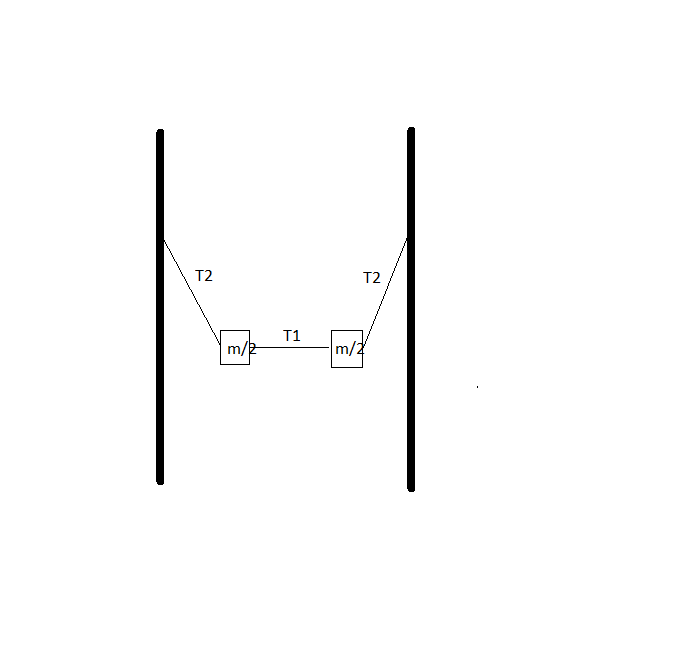
The angle made by string with the wall is same θ
Hence T 2 c o s θ = 2 m g
T 1 = T 2 s i n θ
T 1 = 2 m g t a n θ