JEE Mains Mechanics (Equilibrium) 2
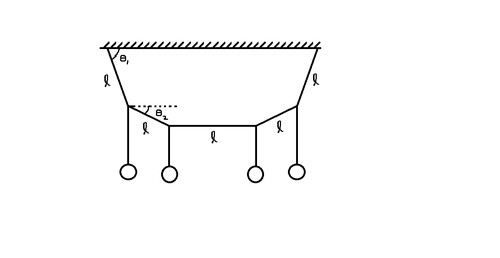 Four identical metal balls are hanging from a light string of length
at equally placed points as shown in figure. The ends of the string are attached to a horizontal fixed support. The middle section of the string is horizontal. Calculate
in degrees if
.
Four identical metal balls are hanging from a light string of length
at equally placed points as shown in figure. The ends of the string are attached to a horizontal fixed support. The middle section of the string is horizontal. Calculate
in degrees if
.
This problem is a part of My Picks for JEE Mains 1
The answer is 45.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Above, you can see the forces acting on each end of one of the sections of the string. It is important to note that I denoted the forces going downwards m g because those are their values, not because the weight of the balls are actually acting on those points. You can also note that the tension T 2 is equal in both ends, because it is said that is a light string.
We can now write Newton's second law for both ends as
Eq. 1: T 1 sin θ 1 − T 2 sin θ 2 − m g = 0
Eq. 2: T 2 cos θ 2 − T 1 cos θ 1 = 0
Eq. 3: T 2 sin θ 2 − m g = 0
Note the sum of forces on the horizontal direction of the lower end has not been written. Replacing the value of m g taken from Eq. 3 on Eq. 1 and re-writing Eq.1 and 2 we obtain
T 1 sin θ 1 = 2 T 2 sin θ 2
T 1 cos θ 1 = T 2 cos θ 2
If we divide these equations we get
tan θ 1 = 2 tan θ 2
Since tan θ 1 = 2 , then tan θ 2 = 1 , which of course gives the answer of θ 1 = 4 5 degrees.