JEE Novice - (14)
tan ( 1 0 7 n ) ∘ = cos 9 6 ∘ − sin 9 6 ∘ cos 9 6 ∘ + sin 9 6 ∘
Find the smallest positive integer n that satisfies the above equation.
This question is a part of JEE Novices .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
More generally (in a similar manner as shown above),
tan ( 4 5 ∘ + α ) = cos α − sin α cos α + sin α .
Since tan 3 2 1 ∘ = tan ( − 3 9 ∘ ) , n can be a negative real number and does not have a defined minimum. It must be specified as an integer.
Log in to reply
If n is an integer , it does not have a minimum value. As (321-180*107k) can be equal to 107n for every integer k. it must be said that n is a natural number
Moderator note:
Good observation with the tangent sum and product formula.
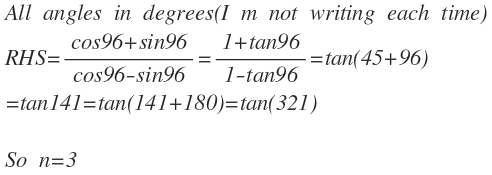
cos 9 6 ∘ − sin 9 6 ∘ cos 9 6 ∘ + sin 9 6 ∘ ⇒ n = 2 1 cos 9 6 ∘ − 2 1 sin 9 6 ∘ 2 1 cos 9 6 ∘ + 2 1 sin 9 6 ∘ = cos 4 5 ∘ cos 9 6 ∘ − sin 4 5 ∘ sin 9 6 ∘ sin 4 5 ∘ cos 9 6 ∘ + cos 4 5 ∘ sin 9 6 ∘ = cos 1 4 1 ∘ sin 1 4 1 ∘ = tan 1 4 1 ∘ = tan ( 1 4 1 ∘ + 1 8 0 ∘ ) = tan 3 2 1 ∘ = tan ( 1 0 7 ∘ × 3 ) = 3