Logarithm System
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ lo g x w lo g y w lo g x y z w = = = 2 4 4 0 1 2
If x , y , z are real numbers greater than 1 and w is a positive number satisfying the system above, then find the value of ( lo g w z ) − 1 .
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
Bonus question: Would the answer change if I remove the line "greater than 1" from the problem statement?
Thanx sir , Actually i made one silly mistake in fourth step.......................................
Yeah. I did the same :)
Clever solution.
If that line will be remove I have to add some conditions to the answer. In particular x>0 y> 0 x>0 and oslo x,y,xyz couldn't be equal to one.
no,the answer would be same in every case except x=0
Direct approach:
w=x^24=y^40=x^12y^12z^12
x^24=y^40 implies x^3=y^5
x^12=(x^3)^4=(y^5)^4=y^20
W=x^12y^12z^12=y^20y^12z^12 =y^32z^12=y^40
Therefore z^12=y^40/y^32=y^8
Implies z^60=y^40=w
Therefore z=w^(1/60)
Therefore log z (base w)=1/60
implies 1/logz (base w)=60
Using the fact that: log a (b) = 1/ log b (a) we can write:
log w (xyz) = 1/ log xyz (w) = 1/12
log w (xyz) = log w (x) + log w (y) + log w (z) = 1/24 + 1/40 + log w (z)
Combining the 2 above, we get
1/12 = 1/24 + 1/40 + log w (z)
1/log w (z) = 60
Should this be a level 4 question?
I placed 0 . 0 1 6 6 6 6 6 6 .... guess it's time to read instructions...
And shouldn't the answer be 0 . 0 1 7 ? Unless it is specifically stated to round down.
EDIT: its fixed
Thats what i think too
Will anyone send a solution because i have answer as 30
Log in to reply
Check out my posted solution above; the answer is indeed 60. :)
l o g x w = 2 4 ...(A)
l o g y w = 4 0 ...(B)
l o g x y z w = 1 2 ...(C)
From (C)
( x y z ) 1 2 = w x 1 2 y 1 2 z 1 2 = w ( x 2 4 ) 2 1 ( y 4 0 ) 1 0 3 z 1 2 = w
From (A) it follows that x 2 4 = w and from (B) it follows that y 4 0 = w
w 2 1 w 1 0 3 z 1 2 = w w 5 4 z 1 2 = w z 1 2 = w 5 1 z 6 0 = w
Therefore, l o g z w = 6 0 and as l o g a b = l o g b a 1 therefore ( l o g w z ) − 1 = l o g z w = 6 0
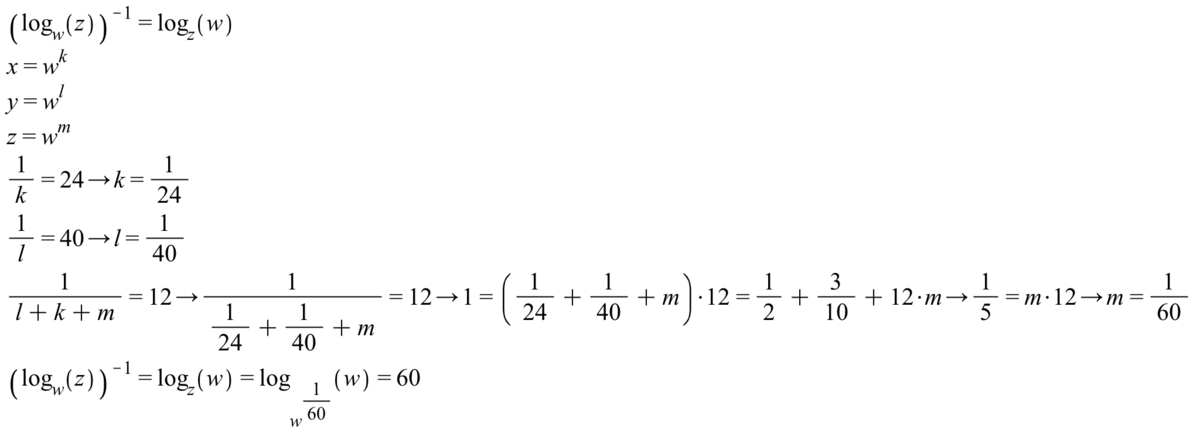
We have that w = x 2 4 = ( x y z ) 1 2 ⟹ x 1 2 = ( y z ) 1 2 .
Since x , y , z are all real numbers greater than 1 we can then conclude that
x = y z ⟹ z = y x , and thus
lo g w ( z ) = lo g w ( x ) − lo g w ( y ) = lo g x ( w ) 1 − lo g y ( w ) 1 = 2 4 1 − 4 0 1 = 6 0 1 .
Therefore ( lo g w ( z ) ) − 1 = 6 0 .