JEE Novice - (22)
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ 1 + z x + y 3 − z x − y = = x 2 − x y + y 2 1 − z + z 2 x 2 + x y + y 2 z 2 + 3 z + 9
If x , y , z satisfy the system of equations above, find the value of z 3 − y 3 .
This question is a part of JEE Novices .
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
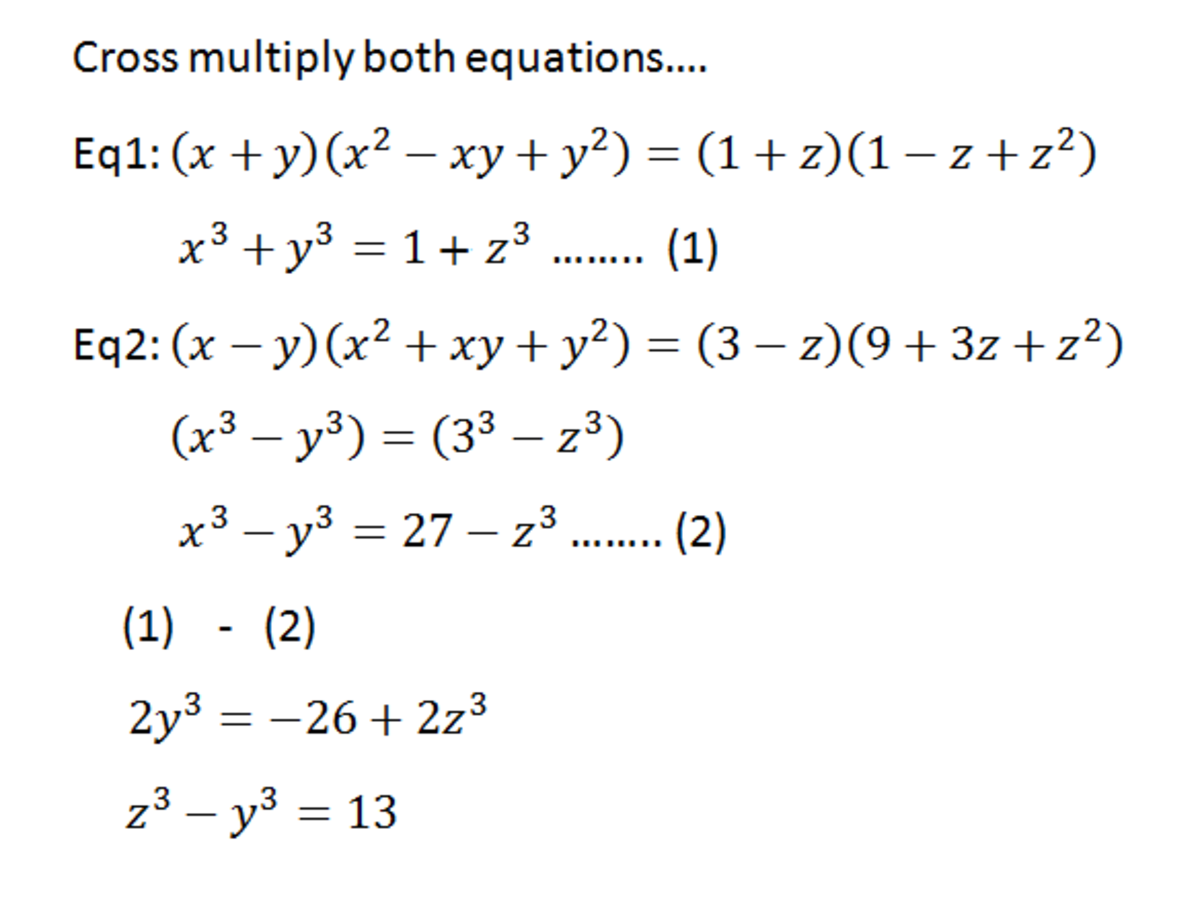
Equation (1) should say x 3 + y 3 = 1 + z 3 .
Nice solution
You can double-check you have the correct sign by finding the sign of the z 3 term, which is z ⋅ z 2 = + z 3 , and finding the x 3 and y 3 terms which are x ⋅ x 2 = + x 3 and y ⋅ y 2 = + y 3 . If you are not short on time, you can expand the brackets. Using the RHS equation 2 for example, 2 7 + 9 z + 3 z 2 − 9 z − 3 z 2 − z 3 = 2 7 − z 3 where all but two of the terms cancel.