JEE Novice - (24) (fixed)
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ x 1 + y 1 = 3 1 x 1 + z 1 = 5 1 y 1 + z 1 = 7 1
If x , y , z satisfy the system above , find the value of the ratio y z .
This question is a part of JEE Novices .
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
There's a slightly easier solution without finding the value of x . Hint: Add them all up.
x 1 + y 1 = 3 1 . . . ( 1 )
x 1 + z 1 = 5 1 . . . ( 2 )
y 1 + z 1 = 7 1 . . . ( 3 )
Adding all 3 equations gives:
x 2 + y 2 + z 2 = 1 0 5 7 1
x 1 + y 1 + z 1 = 2 1 0 7 1
E q u a t i o n 1 ⇒ z 1 = 2 1 0 1
E q u a t i o n 2 ⇒ y 1 = 2 1 0 2 9
z 1 y 1 = 2 1 0 2 9 2 1 0 1
y z = 2 9
As Challenge Master noted, here's an alternative solution which doesn't require finding the value of any of the unknowns.
y z = z − 1 y − 1 = 2 z − 1 2 y − 1 = [ ( y − 1 + z − 1 ) − ( x − 1 + y − 1 ) + ( x − 1 + z − 1 ) ] [ ( y − 1 + z − 1 ) − ( x − 1 + z − 1 ) + ( x − 1 + y − 1 ) ] = 7 − 1 − 3 − 1 + 5 − 1 7 − 1 − 5 − 1 + 3 − 1 = 1 0 5 ( 7 − 1 − 3 − 1 + 5 − 1 ) 1 0 5 ( 7 − 1 − 5 − 1 + 3 − 1 ) = 1 5 − 3 5 + 2 1 1 5 − 2 1 + 3 5 = 1 2 9 = 2 9
Moderator note:
Yes, the faster way is to treat x 1 , y 1 , z 1 as variables a , b , c and solve the system of linear equations. This approach of choosing the correct variables can simplify the working.
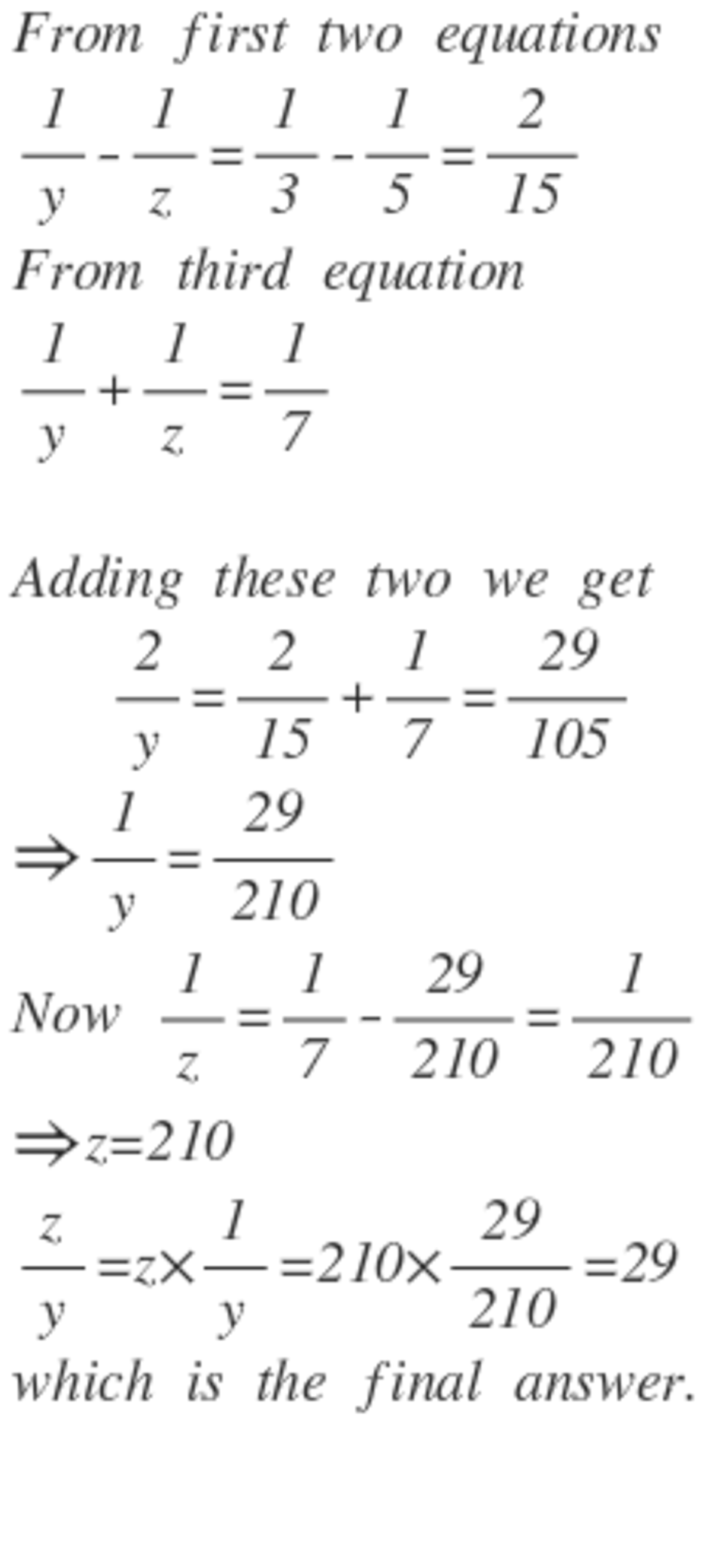
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ x 1 + y 1 = 3 1 x 1 + z 1 = 5 1 y 1 + z 1 = 7 1 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
Eq.1 + Eq.2 − Eq.3: x 2 = 3 1 + 5 1 − 7 1 ⇒ x 1 = 2 1 0 4 1
Eq.1: y 1 = 3 1 − 2 1 0 4 1 ⇒ y 1 = 2 1 0 2 9
Eq.2: z 1 = 5 1 − 2 1 0 4 1 ⇒ z 1 = 2 1 0 1
⇒ y z = 2 9 2 1 0 2 1 0 = 2 9