JEE Novice - (4)
∣ x − 1 ∣ = ∣ x − 2 ∣ + ∣ x − 3 ∣
How many solutions for x does the above equation has if x is a real number?
This question is a part of JEE Novices .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
Simple approach to solve absolute value equations.
Graphical Approach :
Let ∣ x − 1 ∣ = f ( x ) and ∣ x − 2 ∣ + ∣ x − 3 ∣ = g ( x )
No. of real solutions of the equation f ( x ) = g ( x ) will be equal to the no. of points at which the graphs of y = f ( x ) and y = g ( x ) will intersect .
So lets, draw the graphs :
As clear from the graph above, the total number of solutions of the equation
:
(
∣
x
−
1
∣
=
∣
x
−
2
∣
+
∣
x
−
3
∣
)
is
2
enjoy !
Moderator note:
Can you solve this without graphing?
Yeah , drawing graphs is the simplest and time saving way of solving this problem , instead of check various cases by algebra.
Log in to reply
awesome problem
The problems were really amazing, I truly enjoyed them, and for this you recieve C H E E R S ! ! ! from me!
I'm sorry that I'm not able to post solutions as I am confined to a small screen, Keep up the good work and post harder problems! ⌣ ¨
P.S: Honestly I think I talked more than my age requirements!
how did you make the g(x) graph
There's a very simple approach by dividing the real number line into regions, namely,
x ≤ 1 , 1 ≤ x ≤ 2 , 2 ≤ x ≤ 3 , x ≥ 3
For each region, you can transform the given equation into a linear equation in one variable, then solve them and accept the solution if they fall within the region being examined.
The four cases give solutions x = 4 , x = 2 , x = 2 , x = 4 respectively. Matching these solutions with their respective examined regions, we conclude that the only real solutions are x = 2 , 4 .
can you tell me how did you draw its graph??????????
Same approach by me
Moderator note:
Why are you checking for only range of x in 2 < x < 3 and x > 3 ? Are you sure that there's no other solution outside that range?
See Manish Dash's solution for a proper approach.
If your ipothesis is 2<x<3, the solution x=2 is not possible... You're right but with wrong demonstration... :-)
Log in to reply
Oh, you're absolutely right. Thank you Ernesto! :) It was a typo mistake. A better hypothesis could be: " 1<x<3" (from that we notice that "2" is the only integer under that condition, so it works fine with the expression). If 1<x<3 then, |x-1| = x-1 , |x-2| = 0 (since x=2) And |x-3| = -x+3
What is fox theorem
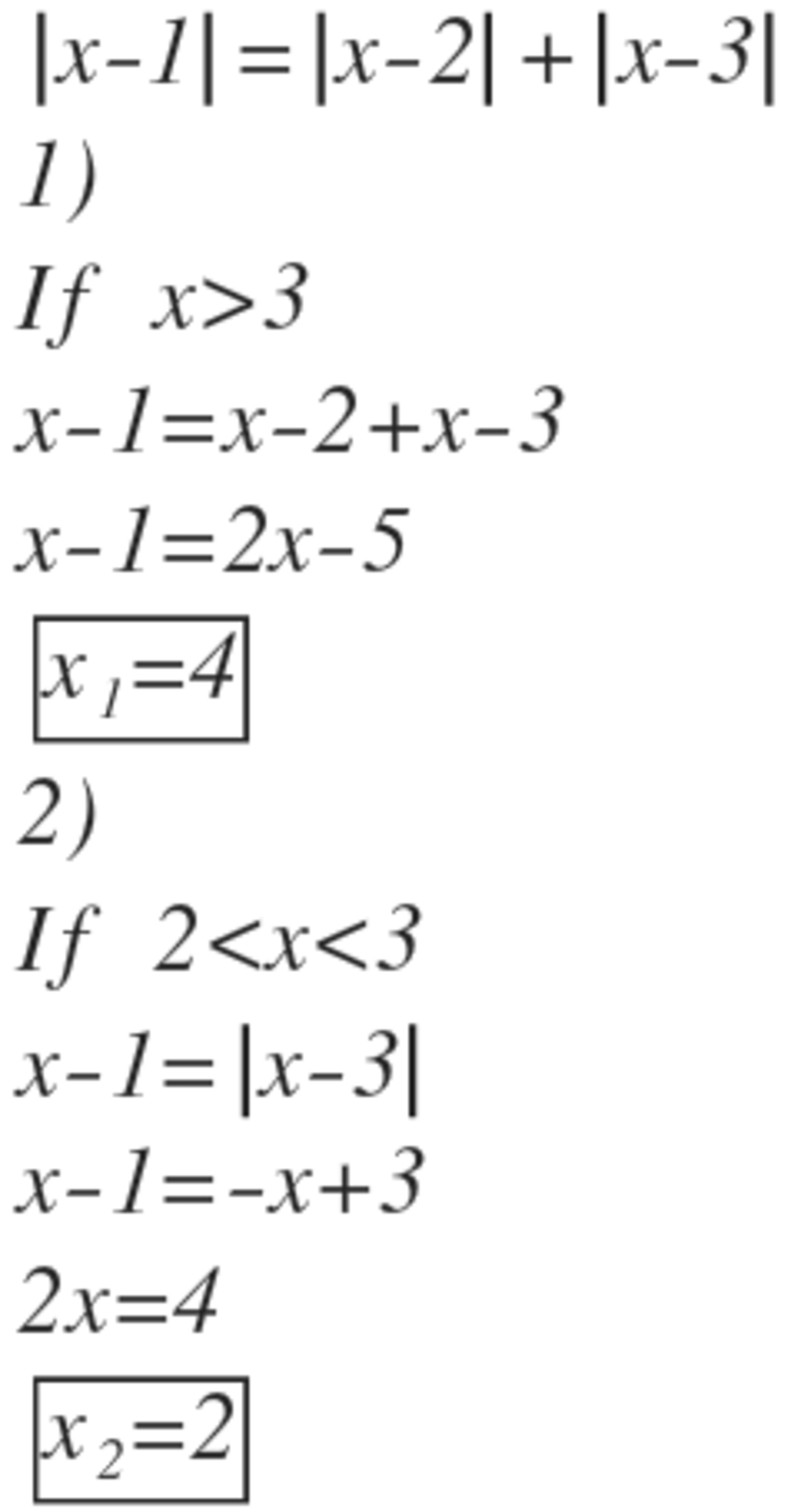
Consider the following cases:
Case 1 If x ≥ 3
x - 1 = (x - 2) + (x - 3)
=> x = 4
Case 2 If 2 ≤ x < 3
x - 1 = (x - 2) - (x - 3)
=> x = 2
Case 3 If 1 ≤ x < 2
x - 1 = - ( x - 2) - ( x - 3)
=> x = 2
Case 4 If x < 1
-(x - 1) = - ( x - 2 ) - ( x - 3 )
=> x = 4
Hence the given equation has 2 solutions: 2 and 4