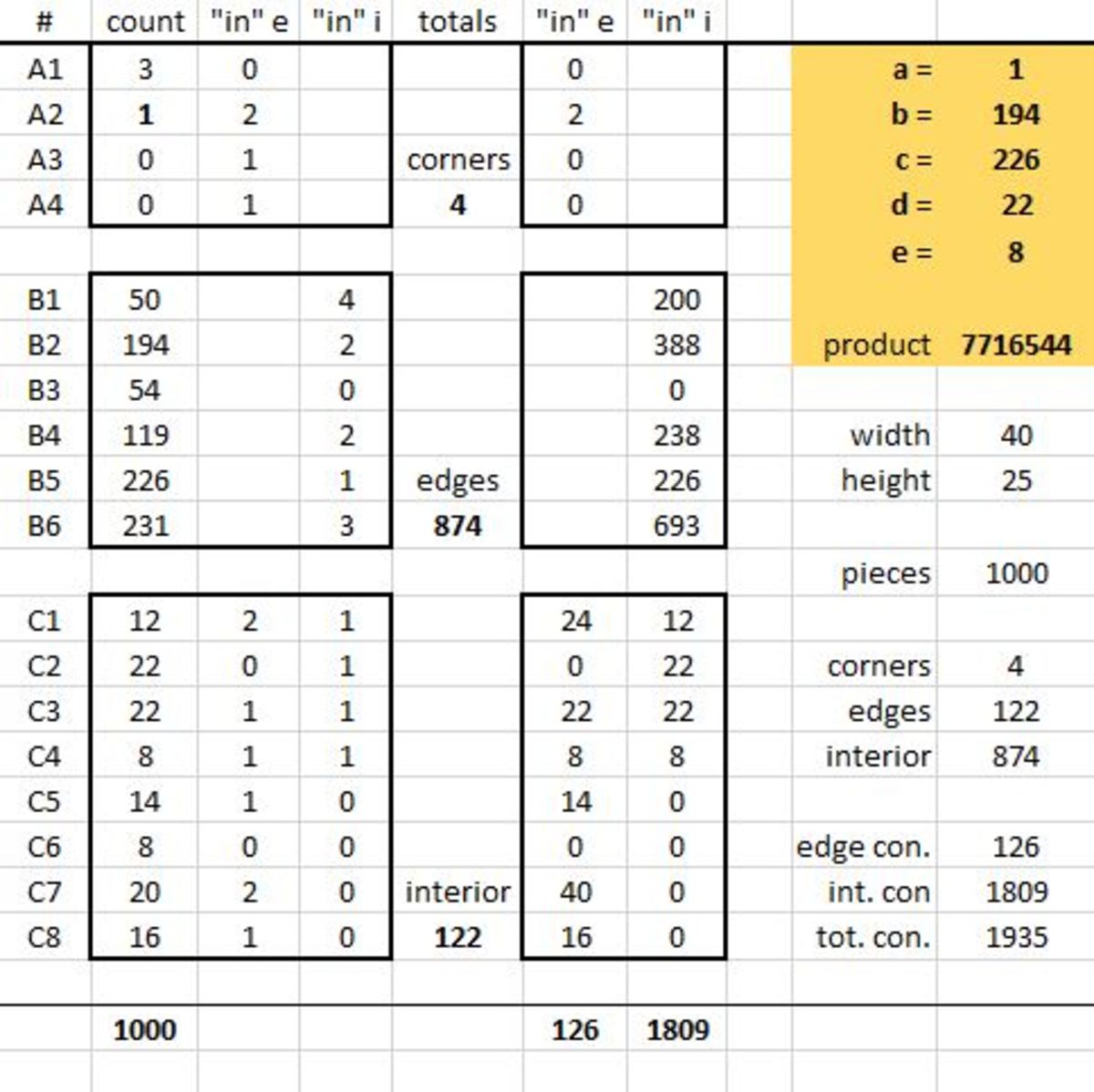
Jigsaw Inventory

The puzzle has $40\cdot 25 = 1000$ pieces, of which

• 4 corner pieces,

• $2\cdot(38+23) = 122$ edge pieces, and

• $38\cdot 23 = 874$ interior pieces.

Combining this with the information in each row in the diagram, we have $\begin{cases} 3+a = 4 & \therefore a = 1 \\ 454+b+c = 874 & \therefore b+c = 420 \\ 92+d+e = 122 & \therefore d+e = 30\end{cases}$

Let's work on the edges first ( $d$ and $e$ ). There are $2\cdot (24+39) = 126$ edge/edge and edge/corner connections, and each of these connections has an "in" and an "out". We will therefore count the "in" connectors in the corner pieces and along the side of the edge pieces. $126 = \#\text{edge "in"} = 2 + 2\cdot 12 + d + 8 + 14 + 2\cdot 20 + 16 = 104 + d.$ It follows that $d = 126 - 104 = 22$ and $e = 30 - d = 8$ .

Now we apply the same method for the remaining $23\cdot 39 + 24\cdot 38 = 1809$ connections. This time we count the "in" connectors of the interior pieces, as well as the "in" connectors of the edge pieces opposite the edge. $1809 = \#\text{interior "in"} = (12+22+22+8) + (4\cdot 50 + 2\cdot b + 2\cdot 119+ c + 3\cdot 231) \\ 1809 = 1195 + 2b + c\ \ \ \ \therefore\ \ \ \ 2b+c = 614.$ We already knew that $b + c = 420$ , so a simple subtraction shows that $b = 614 - 420 = 194$ and $c = 420 - 194 = 226$ .

The answer is therefore $\boxed{1\cdot 194\cdot 226\cdot 22\cdot 8 = 7\:716\:544}$ .

And here is a little spreadsheet I used to check if the numbers work out: