Jigsaw Area
The shape of this jigsaw puzzle piece may be viewed as a square of side to which four circles of radius have been added. The square and the circles overlap. Assume that the part of the circle circumference that sticks out forms an arc.
The total area of the puzzle piece may be written as Calculate the value of .
The answer is 10.10963.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Think of each connector as a circle sector ("pie", or here more like a Pacman shape) with an isosceles triangle:!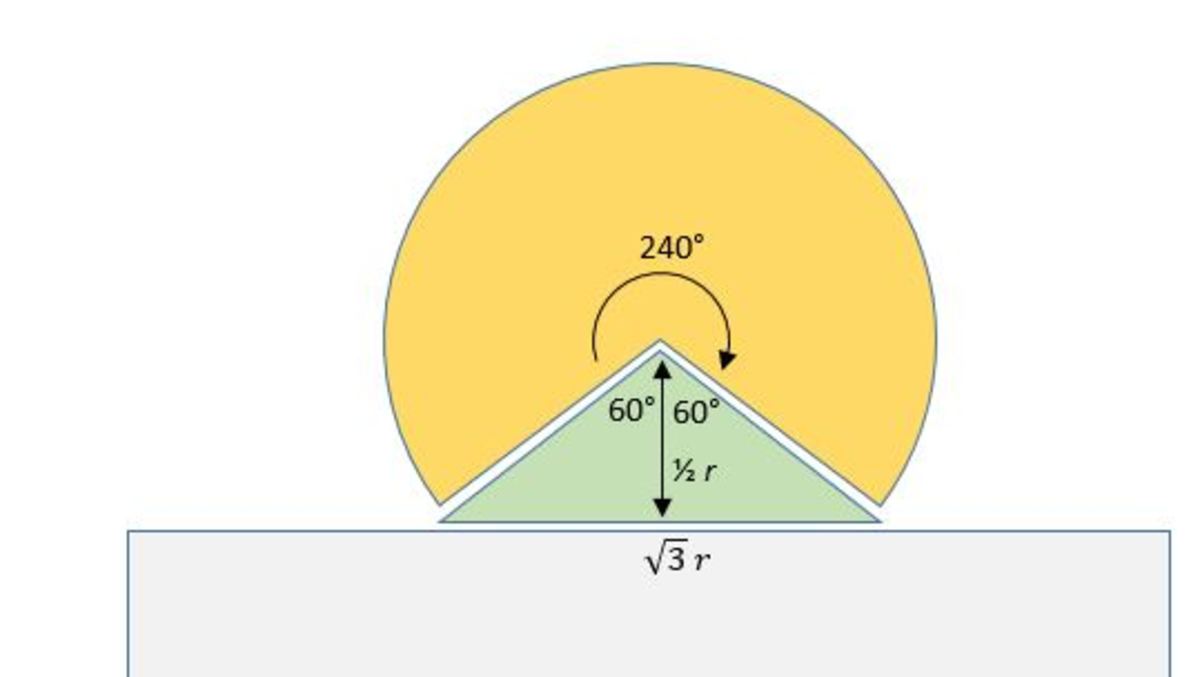 The area of the circle sector is
3
6
0
∘
2
4
0
∘
⋅
π
r
2
=
3
2
π
r
2
;
the triangle has a width of
2
⋅
r
sin
6
0
∘
=
3
r
and a height of
r
cos
6
0
∘
=
2
1
r
, with area
2
1
⋅
3
r
⋅
2
1
r
=
4
1
3
r
2
.
Adding these areas together and multiplying by four, we find for the total area of the four connectors
4
⋅
(
3
2
π
r
2
+
4
1
3
r
2
)
=
(
3
8
π
+
3
)
r
2
.
It follows that
c
=
3
8
π
+
3
≈
1
0
.
1
0
9
6
3
.
The area of the circle sector is
3
6
0
∘
2
4
0
∘
⋅
π
r
2
=
3
2
π
r
2
;
the triangle has a width of
2
⋅
r
sin
6
0
∘
=
3
r
and a height of
r
cos
6
0
∘
=
2
1
r
, with area
2
1
⋅
3
r
⋅
2
1
r
=
4
1
3
r
2
.
Adding these areas together and multiplying by four, we find for the total area of the four connectors
4
⋅
(
3
2
π
r
2
+
4
1
3
r
2
)
=
(
3
8
π
+
3
)
r
2
.
It follows that
c
=
3
8
π
+
3
≈
1
0
.
1
0
9
6
3
.