Jmetry1
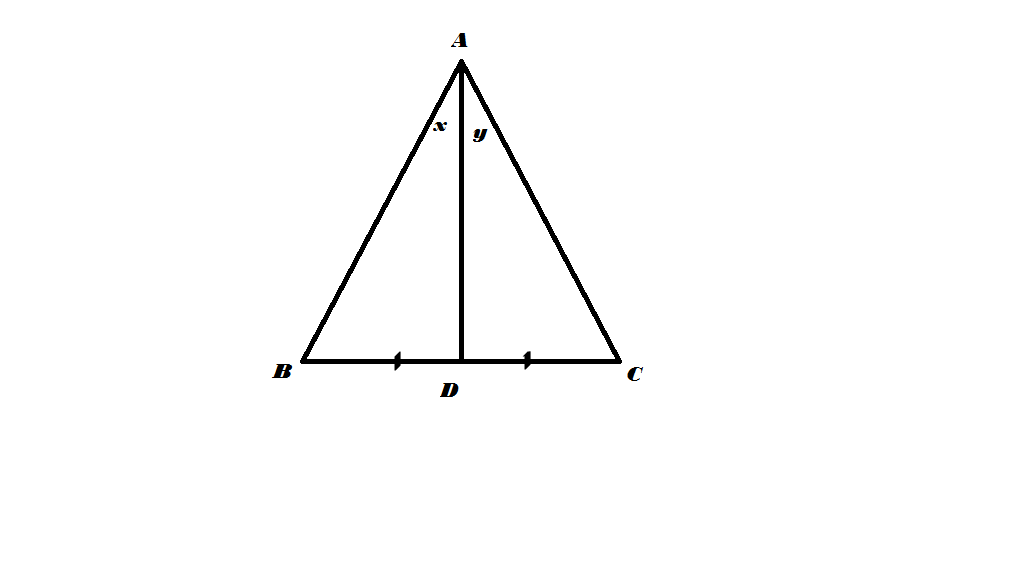
In the above triangle ABC, AD is the median from A. Angle x = 4 5 ∘ and angle y = 3 0 ∘ .Find the value of A C A B ?
Note:The answer is of the form a 1 .Enter the value of a .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Sir, your solution was really great.Please see if mine is correct.
Log in to reply
Sir there is a small typo i guess..it should be AC instead of AB in the second eq.
I think your solution is better.
Log in to reply
Thank you sir.I have learnt much from your solutions.
Since AD is the median area of triangle ABD=ACD
therefore
2 1 ∗ A B ∗ A D ∗ s i n x ∘ = 2 1 ∗ A C ∗ A D ∗ s i n y ∘
Hence
A C A B = s i n x ∘ s i n y ∘ = s i n 4 5 ∘ s i n 3 0 ∘
A C A B = 2 2 = 2 1
Thanks for your answer.
First we replace the distance BD and BC with X. Then we split up triangle ABC into Triangles ABD and ACD. Then we can use the definition of Sin (Length of Opposite side/Length of Hypotenuse) to solve for AC and AB in terms of X.
Sin(45)=X/AB (This is the definite of Sin)
Sin(45)=2^{1/2}/2 (using Calculator or Unit Circle)
2^{1/2}/2=X/AB (Transitive Property)
2^{1/2}/2X=1/AB (Divide both sides by X)
2X/2^{1/2}=AB (Raise both sides ^-1)
Sin(30)=X/AC
Sin(30)=1/2
1/2=X/AC
1/2X=1/AC
2X=AC
Now that we have Solved for AB and AC, We can Plug them in to AB/AC to get the final answer.
AB/AC=2X/{2^1/2}/2X (Plug in AB and AC found above)
AB/AC=1/(2^1/2) (Cancel out the 2X from the Top and bottom of the equation
Now we look at how the problem wants us to Format the answer.
1/(a^1/2)=1/(2^1/2) (place the format of the answer equal to our format of AB/BC)
a^1/2=2^1/2 (Raise both side to ^-1)
a=2 (Raise both sides to ^2)
The Answer is 2.
(I'm not sure how to Edit things to make them appear more like Math Equations and less like horizontal text. I tried to use the formatting guide but It only seemed to work for Bolding things.)
Let ∠ A D B = θ . Using Sine Rule, we have:
⎩ ⎪ ⎨ ⎪ ⎧ sin θ A B = sin 4 5 ∘ B D sin ( 1 8 0 ∘ − θ ) A C = sin 3 0 ∘ D C A B = 2 B D sin θ A C = 2 D C sin ( 1 8 0 ∘ − θ ) = 2 D C sin θ
A C A B = 2 D C sin θ 2 B D sin θ = 2 2 = 2 1 [ B D = D C ]