Just The Right Amount Of Shades

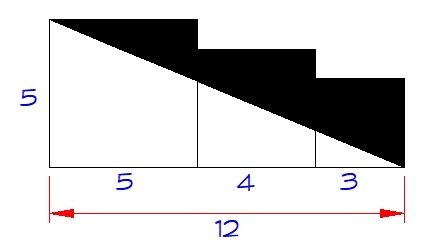
The figure above shows three consecutive squares of sides 5, 4 and 3, respectively.
Find the area of the black region.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
I did it the same way :)
Consider the middle square to be a 4×5 rectangle from which a 1 × 4 rectangle is cut. So, the area cut is 1 × 4 = 4.
Similarly consider the right square to be a 3 × 5 rectangle from whicn a 2 × 3 rectangle is cut. So, area cut is 2 × 3 = 6.
Now, look at the initial picture which consists of a 5×5 square, 4×5 rectangle and 3×5 rectangle. It looks like a 12 × 5 rectangle. Its diagnol divides it into 2 parts:- upper part and down part. And the rectangles are cut from the upper and shaded part. So, the area of the shaded part is
Area of shaded triangle formed by diagnol (Upper part) - Area of rectangles cut
=
(
2
1
×
1
2
×
5
)
−
(
4
+
6
)
=
(
3
0
−
1
0
)
=
2
0
.

yup.. did it in a similar manner. Nice explanation ..+1.
A = Area of the three squares - Area of the triangle
A = 5 2 + 4 2 + 3 2 − 2 1 ( 5 ) ( 1 2 ) = 2 0
This is my own solution. I am using a new account now.
area of the black region = area of the three squares - area of the big triangle
area of the three squares = 25 + 16 + 9 = 50 square units
area of the big triangle = 1/2 x 5 x (5+4+3) = 1/2 x 5 x 12 = 30 square units
substitute,
area of black region = 50 - 30 = 20 square units
Relevant wiki: Length and Area Problem Solving
The area of the white portion is 30. It would be area of the dark part, if it were a rectangle with the bottom edge of the shaded part as it's diagonal. From the image we can see that the area of the gap above the middle square is 4. Similarly the area of the gap above the small square is 2*3= 6. So the area of the dark part is 30 - 4 - 6 = 20
Area of the total figure = 25+16+9 sq. units Area of the Unshaded triangle = 0.5x(5+4+3)x5 sq. units ∗ ∗ A r e a o f t h e S h a d e d P a r t = 5 0 − 3 0 = 2 0 s q . u n i t s ∗ ∗
Relevant wiki: Length and Area - Composite Figures
Total area of all the squares = 5 2 + 4 2 + 3 2 = 2 5 + 1 6 + 9 = 5 0 Area of the not shaded triangle = 2 1 × base × height . ⟹ A = 2 1 × 5 × 1 2 = 3 0 . Area of shaded region = Total Area − Not Shaded region = 5 0 − 3 0 = 2 0 .