Joining in the path madness

We can put all 12 vertices of an icosahedron into 4 "layers" as follows: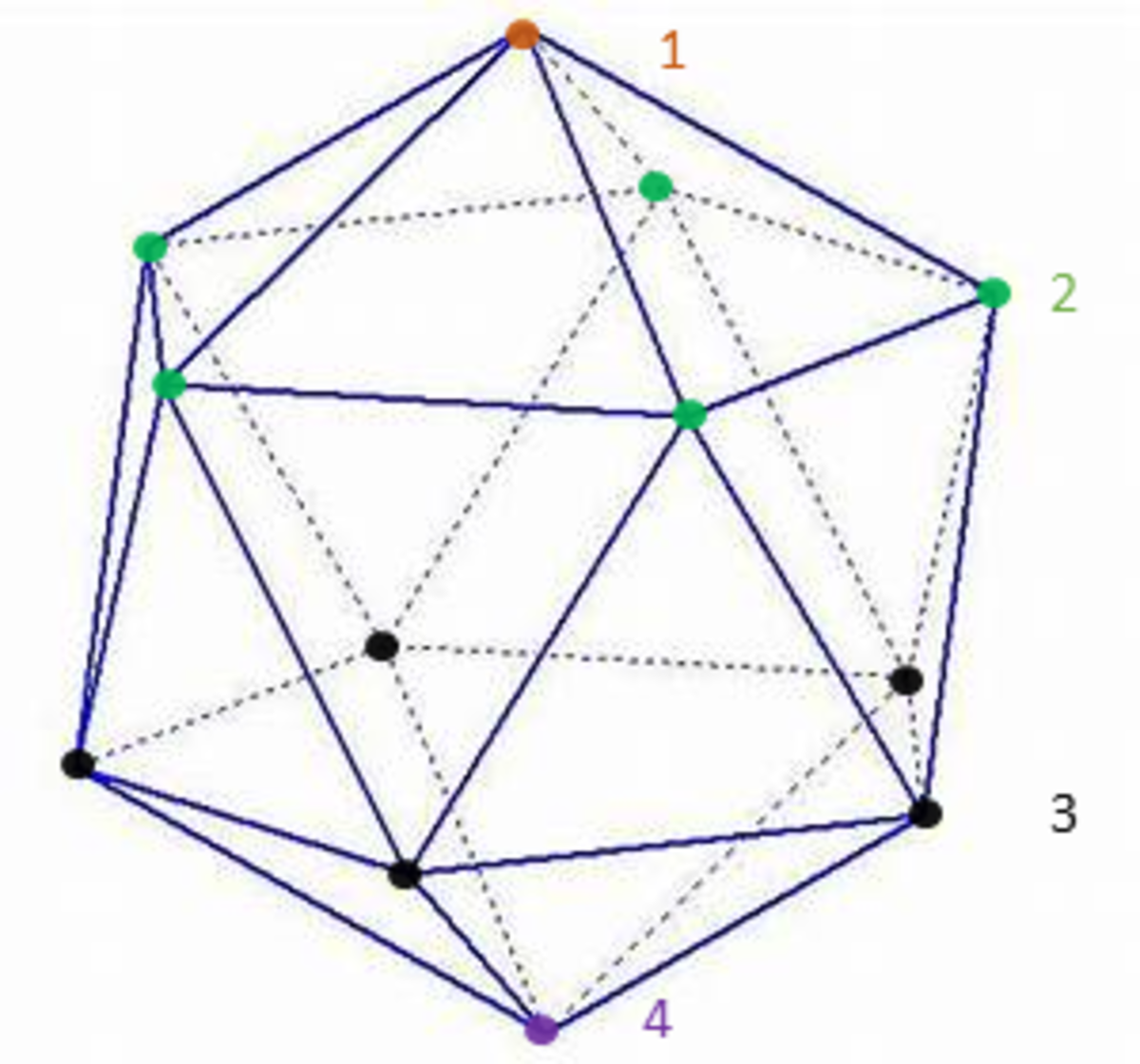 We'll then compute the probability of the ant being on each layer after n steps. Let $p_i^n,\ 1\leq i\leq 4,\ n\in\mathbb{N}$ denote this probability to be on layer i after n steps. With this notation, what we are looking for is $p_1^{10}$ . We'll get recurrence relations using the following observations:

• If you're on layer 1 after n steps, you'll be on layer 2 after one more step. Symmetrically, you can only go to layer 3 if you come from layer 4.

• If you're on layer 2 after n steps, you have one neighbor in layer 1, two neighbors in layer 2 and two neighbors in layer 3. Thus the probability to go to layer 1 is $\frac{1}{5}$ and the probabilities to go to layers 3 and stay on layer 2 are $\frac{2}{5}$ . Same thing for layer 3, but we go to layer 4 instead of layer 1 with probability $\frac{1}{5}$ .

We get the following recurrence equations (you can draw the Markov chain if that helps):

$p_1^{n+1}=\frac{1}{5}p_2^n$

$p_2^{n+1}=p_1^n+\frac{2}{5}p_2^n+\frac{2}{5}p_3^n$

$p_3^{n+1}=\frac{2}{5}p_2^n+\frac{2}{5}p_3^n+p_4^n$

$p_4^{n+1}=\frac{1}{5}p_3^n$

We know we start from layer 1, so we have $p_1^0 = 1$ and $p_2^0=p_3^0=p_4^0=0$ . We can then compute iteratively to get $p_1^{10}$ (manually or with a computer). We get the final result: $m=815365$

PS: Here are all the values needed to compute m: