JOMPC-II
Let a , b and c be positive reals such that a b c = 1 . Find last two digits of the minimum value of ( a + 2 0 1 5 b ) ( b + 2 0 1 5 c ) ( c + 2 0 1 5 a )
Source: JOMPC.
The answer is 96.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Same solution
Did the same way
My Method: :)
WLOG, let a ≥ b ≥ c . By the extreme power of common sense, 2 0 1 5 a ≥ 2 0 1 5 b ≥ 2 0 1 5 c .
Then, by Reverse-rearrangement inequality,
( a + 2 0 1 5 b ) ( b + 2 0 1 5 c ) ( c + 2 0 1 5 a ) ≥ ( a + 2 0 1 5 a ) ( b + 2 0 1 5 b ) ( c + 2 0 1 5 c )
( a + 2 0 1 5 b ) ( b + 2 0 1 5 c ) ( c + 2 0 1 5 a ) ≥ ( 2 0 1 6 a ) ( 2 0 1 6 b ) ( 2 0 1 6 c )
( a + 2 0 1 5 b ) ( b + 2 0 1 5 c ) ( c + 2 0 1 5 a ) ≥ 2 0 1 6 3 a b c . Since abc = 1,
( a + 2 0 1 5 b ) ( b + 2 0 1 5 c ) ( c + 2 0 1 5 a ) ≥ 2 0 1 6 3 .
Then, finding the last three digits of 2 0 1 6 3 is the same as finding the last three digits of 1 6 3 . So, last three digits of 1 6 3 are the last three digits of 4 0 9 6 which are 9 6
By coincidence, I was studying the Reverse-rearrangement inequality when I saw this problem.
hey you are so good in inequality , keep rocking!
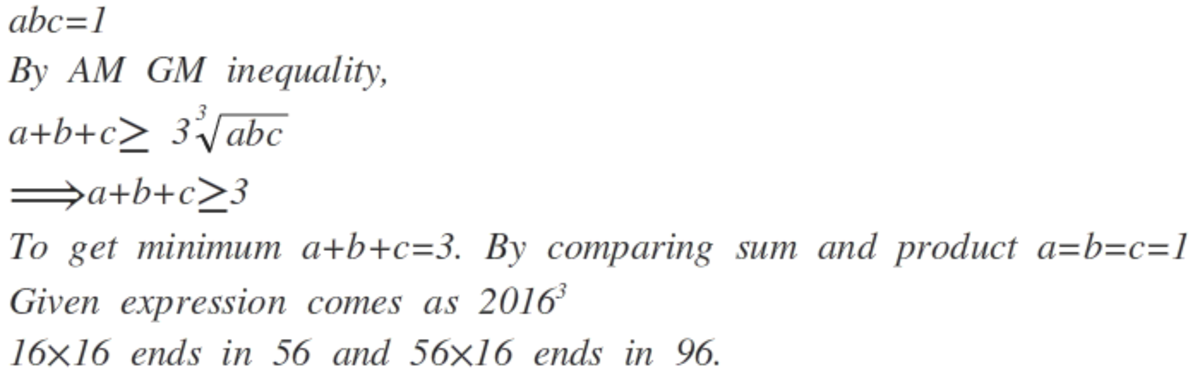
Wrong method :
Using AM-GM:
a + 2 0 1 5 b ≥ 2 2 0 1 5 a b b + 2 0 1 5 c ≥ 2 2 0 1 5 b c c + 2 0 1 5 a ≥ 2 2 0 1 5 c a ⟶ ( a + 2 0 1 5 b ) ( b + 2 0 1 5 c ) ( c + 2 0 1 5 a ) ≥ 8 2 0 1 5 3 .
But this is not possible because for equality to hold we must have a = 2 0 1 5 b , b = 2 0 1 5 c , c = 2 0 1 5 a which is absurd as it will give on multiplying a b c = ( 2 0 1 5 ) 3 a b c
Correct method :
Using AM-GM:
a + 2 0 1 5 t i m e s b + b + . . . . . . + b ≥ 2 0 1 6 2 0 1 6 a b 2 0 1 5 b + 2 0 1 5 t i m e s c + c + . . . . . . + c ≥ 2 0 1 6 2 0 1 6 b c 2 0 1 5 c + 2 0 1 5 t i m e s a + a + . . . . . . + a ≥ 2 0 1 6 2 0 1 6 c a 2 0 1 5 ⟶ ( a + 2 0 1 5 b ) ( b + 2 0 1 5 c ) ( c + 2 0 1 5 a ) ≥ 2 0 1 6 3
And equality holds when a = b = c = 1 .