Juggling Logs

Algebra Level 2

Suppose

$\Large \log_{b^p} (\log_{b^q} x) = \log_{b^r} (\log_{b^s} x)$

for positive numbers $p$ , $q$ , $r$ , and $s$ such that $p < r$ .

Which of the following is the best solution for $x$ ?

\large x = b^{\frac{q^{r/(r-p)}}{s^{p/(r-p)}}}

\large x = b^{\frac{pqrs}{r-p}}

\large x = b^{(\frac{q}{s})^{\frac{r}{p}}}

\large x = b^{\frac{qr}{ps}}

3 solutions

David Vreken
Apr 13, 2019

Let $x = b^n$ . Then

$\log_{b^p} (\log_{b^q} x) = \log_{b^r} (\log_{b^s} x)$

$\log_{b^p} (\log_{b^q} b^n) = \log_{b^r} (\log_{b^s} b^n)$

$\log_{b^p} (\log_{b^q} b^{q\frac{n}{q}}) = \log_{b^r} (\log_{b^s} b^{s\frac{n}{s}})$

$\log_{b^p} (\frac{n}{q}) = \log_{b^r} (\frac{n}{s})$

$(\frac{n}{q})^r = (\frac{n}{s})^p$

$n = \frac{q^{r/(r-p)}}{s^{p/(r-p)}}$

So $x = b^n = b^{\frac{q^{r/(r-p)}}{s^{p/(r-p)}}}$

Sachu Verma
Apr 14, 2019

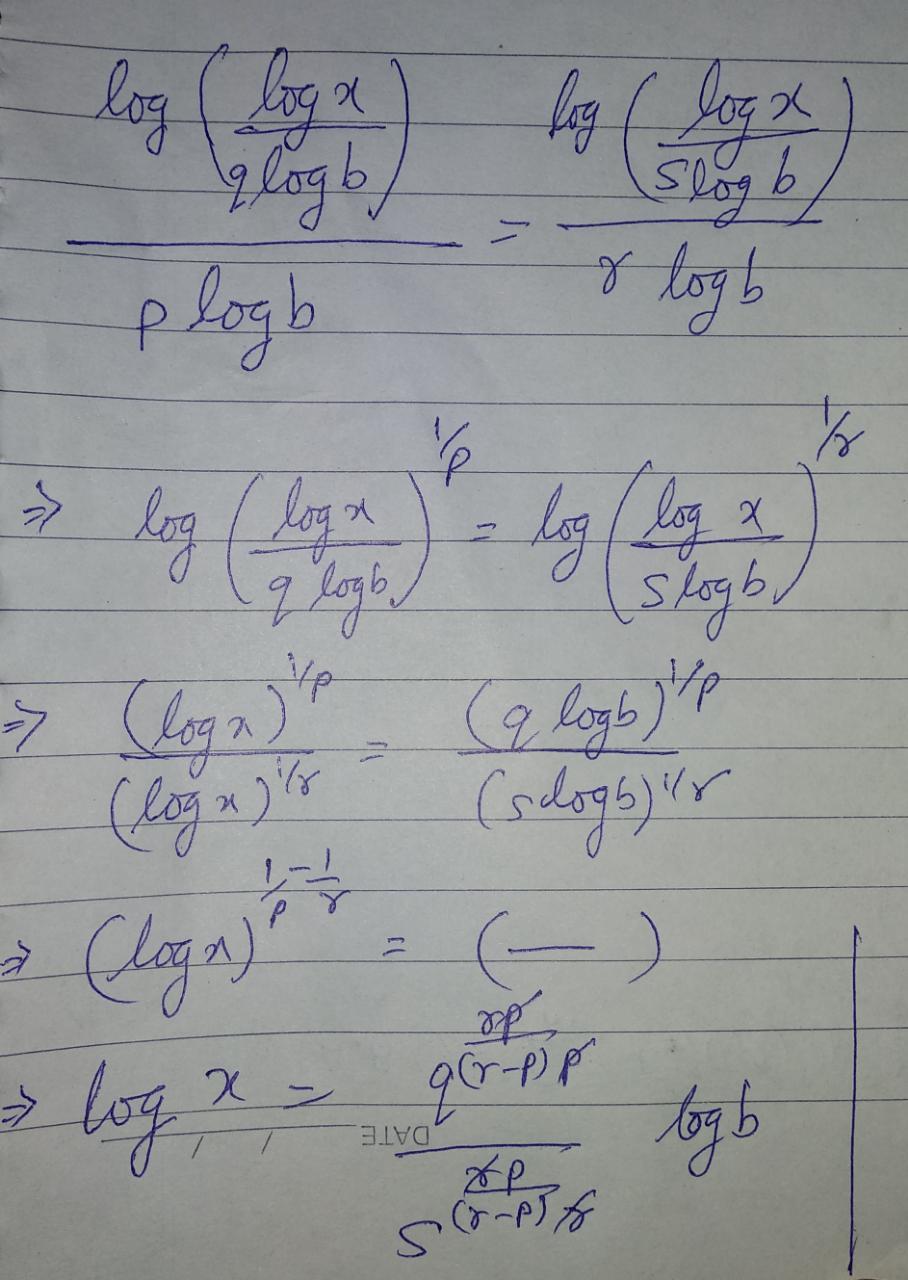in the end again cancelling both side logs we will get value of x

A Former Brilliant Member
Apr 10, 2019

Make use of the property : logarithm of a to the base b is log(a)/log(b). Then a few algebraic steps lead to the answer.