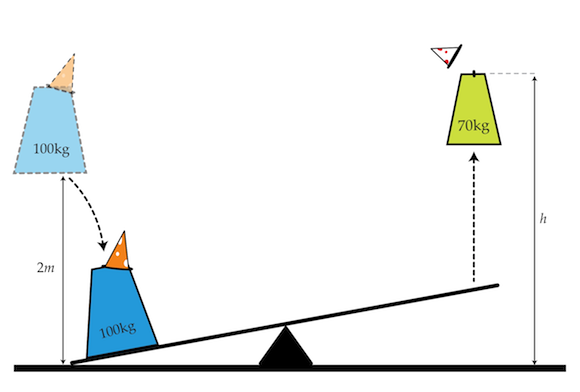
Jumping clowns

Step 1: $v^2=u^2+2as=0^2+2\times 9.8~\textrm{m/s}^2 \times 2~\textrm{m}=39.2~\textrm{m}^2/\textrm{s}^2$ $~$

Step 2:

$E_k=\frac{1}{2}mv^2=\frac{1}{2} \times 100~\textrm{kg} \times 39.2~\textrm{m}^2/\textrm{s}^2=1960~\textrm{J}$ $~$

Step 3:

$E_k \times \frac{2}{3} = 1960~\textrm{J} \times \frac{2}{3}=\frac{3920}{3}~\textrm{J}$ $~$

Step 4:

$E_k= \frac{1}{2}mv^2=\frac{1}{2} \times 70~\textrm{kg} \times v^2=v^2 \times 35~\textrm{kg}=\frac{3920}{3}~\textrm{J}$

$\therefore v^2=\frac{3920}{3 \times 35}~\textrm{m}^2/\textrm{s}^2=\frac{112}{3}~\textrm{m}^2/\textrm{s}^2$

Step 5:

$v^2=u^2 +2as = 0^2+2\times 9.8~\textrm{m/s}^2 \times s= s \times 19.6~\textrm{m/s}^2$

$\therefore s=\frac{v^2}{19.6~\textrm{m/s}^2}=\frac{\frac{112}{3}~\textrm{m}^2/\textrm{s}^2}{19.6~\textrm{m/s}^2}= \left(\frac{112}{3\times 19.6}\right)~\textrm{m} \approx 1.9~\textrm{m}$

Therefore, the required answer is $\fbox{1.9}$ !

Note:

1. Sorry for being shortcut...

2. That was a nice trick, showing $h$ larger than the left side's height in the picture... I was a bit confused about the answer at first!!!

The first clown used $(100kg)(2m)=200J$ of energy. $\frac{2}{3}$ of that is transferred, which is $\frac{400}{3}J$ . Since the mass of the other clown is $70kg$ , he moved up $\frac{\frac{400}{3}J}{70kg}=\boxed{1.90m}.$

The 1st clown has a mass of 100 kg and height from the ground is 2 m.

$PE_i = mgh$

$PE_i = (100)(9.8)(2)$

$PE_i = 1960 J$

The 2nd clown has a mass of 70 kg and the height is unknown.

$PE_f = \frac{2}{3} PE_i$

Thus,

$PE_f = 1306.67 J$

$PE_f = mgh$

$h = \frac{PE_f}{mg}$

$h = \frac{1306.67}{(70)(9.8)}$

$h = 1.9 m$

Energy of 7oKg clown = 2/3 of energy of 100 kg clown 70xgxh= 2/3x2xgx2 on solving for h, h = 1.904m

Total potential energy of first clown at the beginning was $100\times 2 \times g = 200g$ . $\frac23$ of the energy was lost, so we are left with $\frac{400g}{3}$ joules of energy for the second clown. Now, this energy equals the potential of the second clown at the highest point which is $70hg$ . Equating the two, canceling the $g$ s and solving for $h$ gives us our answer $1.9$

The gravitational energy of the first clown can be calculated by

$GPE = 100 \cdot g \cdot 2 = 200 \cdot g$

Since $\frac23$ of the first clown's energy is transferred to the second clown, then the second clown will have $\frac23 \cdot 200 \cdot g = \frac{400}{3} \cdot g$ gravitaitonal potential energy. To find the height of the second clown, we do:

$\frac{400}3 \cdot g = 70 \cdot g \cdot h$

Rearranging for h, we find that:

$h = \frac{400}{21} \approx \fbox{1.9}$