Jumping to Conclusions ?
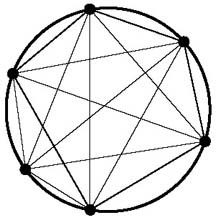Place 12 points along a unit circle, in such a way that when you draw all lines connecting every pair of points, no more than two lines pass through any interior point.
In other words 12 points on the circumference are joined by chords with no three internally concurrent.
How many regions does this divide the circle into?
For e.g.
1 point you get 1 region..
2 points you get 2 regions
3 points you get 4 regions
4 points you get 8 regions
5 points you get 16 regions...
The problem is not original.
The answer is 562.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
According to Euler's formula for the number of regions, F = E - V + 2.
CHORDS --- Each chord is determined by two points on the circle, and there are nC2 ways to choose two of these n points. Hence there are nC2 chords.
FACES -- The number of faces is equal to the number of regions except there is also a face formed by the region outside the circle. So (F+1) = E - V +2.
Thus F = E - V +1
Every four points on the circumference uniquely define an intersection point of two chords. Conversely, any intersection point of two chords gives a unique set of four points (with the two chords being diagonals of respective quadrangle). Let there be n points on the circle
VERTICES --- Thus there are V = nC4 vertices inside the circle + n vertices on the circle. Vertices = n+nC4
EDGES --- Note that there are n edges that are circular arcs. Four edges meet at each of the nC4 vertices making up 4nC4 edges. There are nC2 chords and each chord corresponds to two edges meeting the circle , making 2nC2 edges. We have 4nC4 and 2nC2 edges but each has been counted twice, one for each of the vertices at its ends. Hence there are n + nC2 + 2nC4 edges.
By Eulers formula F = E +1 - V, we derive the regions F as
F = nC4 + nC2 +1
For n=12, we get 562 regions.
This is a classic problem of not jumping to hasty conclusions on limited trials. The geometric series that appears to be till n =5, changes after n=6...