Jumps

Probability Level 2

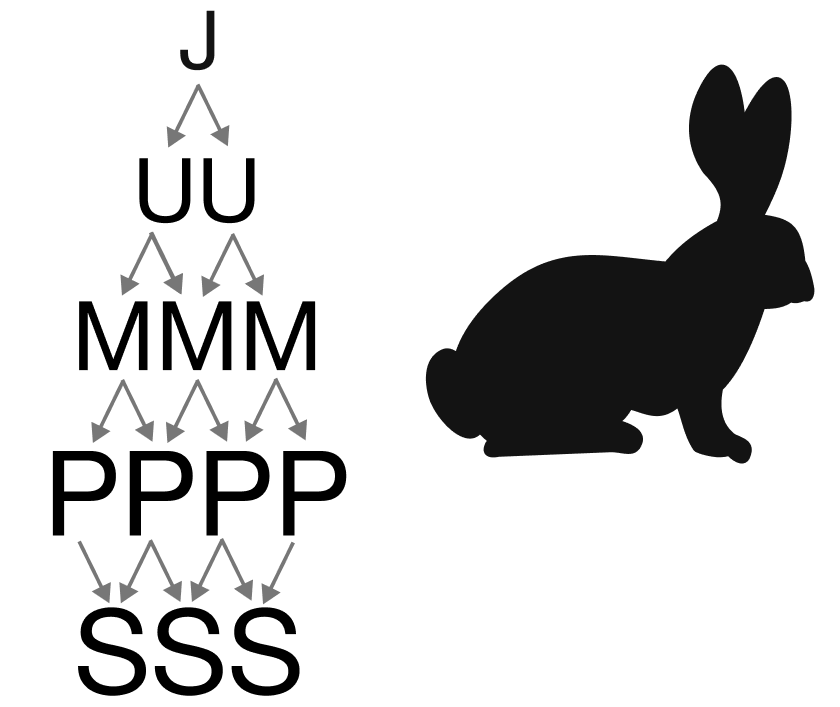
Starting at the "J" and moving down either diagonally left or right each step as shown, how many ways are there to spell the word "JUMPS"?

Note : There are only three S letters in the last row, so the Ps on the far right and left each have only one direction available.

12 14 16 18 20

3 solutions

Jason Dyer Staff
Sep 30, 2016

Without the missing Ss on the bottom: each step has 2 choices, left or right, for a total of $2 \times 2 \times 2 \times 2 = 16$ choices.

The S missing on the far right and far left each exclude 1 route each, so the actual total is $16 - 2 = 14$ choices.

Please I don't understand how it was 2×2×2×2. Since each step has 2 choices I thought it would be 2×2×2×2×2×2×2×2 (that is the 2 routes from J,U,U,M,M,M,P,P) Please explain a little further.

Nwankpa Richard - 3 years, 7 months ago

You have only 4 choices to make when forming a specific word JUMPS. It seems like you're imagining every choice somehow is being included in one word, where some of the routes specifically can't be reached on a certain tracing of the word.

Jason Dyer Staff - 3 years, 7 months ago

yeah pls explain

Saidutt Sharma - 1 year, 5 months ago

I replied to the other one, but I can cut and paste:

Jason Dyer Staff - 1 year, 5 months ago

Think of it as recursion. If you look at how many combination of J-U-M can be made, it is 4. Each individual 'U' has two choices to make, and there are two 'U's (which was accounted for by the previous depth above). Same logic if you keep on going down, since everything is accounted for above, each individual letter of the current level has only 2 choices (except for the P to S at the end)

Kevin Sun - 1 month, 1 week ago

Matt O
Oct 4, 2016

Pascal's Triangle can be used to step through each level and get the number of paths that go through each individual level. The final number is the sum of the numbers in the last row.

1 1

1 2 1

1 3 3 1

4 6 4

@Matt O I couldn't understand. Can you please provide a more detailed explanation?

Ankit Kumar Jain - 4 years, 2 months ago

Consider any letter with arrows pointing towards it. The number of ways to get to that letter is equal to the sum of the number of ways to get to the letters at the head of those arrows. Read up on Pascal's Triangle if you haven't already since it works in a very similar way.

To apply it to this example, start at the top and work your way down.

For the first row, there's only one way to get a J. This is why I mark the row off as 1.

For the second row, for each U in the row there's only only way to get there from the previous row. This is why I mark the row off as "1 1"

Now consider the third row. The Ms at the ends of the row only have 1 way to be reached. The middle M however can be reached for either U. Therefore the number of ways to get to the middle U is 1+1=2.

Repeat this logic to get the answer.

Matt O - 4 years, 2 months ago

ohhh this is smart.

at first I thought you had to use all the numbers in the fifth row of the pascal's triangle but then I realized it was only the middle three numbers.

Laura Gao - 3 years, 2 months ago

Than Win Hline
Jul 16, 2020

We can solve it using Passcal triangle or we can use the rule of sum to count the total path to go from one node to another. J(1) U(1) U(1) M(1) M(2) M(1) P(1) P(3) P(3) P(1) S(4) S(6) S(4)
We just sum up the last row: 4 + 6 + 4 = 14

Jumps

3 solutions

0 pending reports