Just 1-2-3
Which is larger, 3 2 1 or 3 2 1 ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
One divided by two divided by three should be the same as one divided by two divided by three. But it is actually 1/(2/3) and (1/2)/3 not 1/2/3.
Log in to reply
Yes, division is not associative, unlike addition or multiplication. The final result depends on the order in which the numbers are divided.
In the Name of God
1 divide by 2/3 = 1 x 3/2 (idk the reasoning, I was taught at school to do that) = 3/2 .
1/2 divide by 3 = 1/2 divide by 3/1 = 1/2 x 1/3 [The same process as the first calculation above; replacing the division with multiplication, and at the same time, inverting the numerator (upper portion of a fraction) and the denominator (lower part of the fraction); this technique applies only for the right side of our calculations for divisions, according to my experience with this math problem] = 1/6 .
Compare: -> 3/2 = 9/6 = 1.5 -> 1/6 = 1/6 = 0.16667 Conclusion: 3/2 is larger than 1/6.
Log in to reply
Is reducing the fraction to decimal expansion the only way to compare the two quantities?
Do you see how dividing a number by 2 is the same as multiplying it by
2
1
?
We can extend this to: dividing by
3
2
is same as multiplying by
2
3
.
i think that logically the denominator of second is greater thats why its greater
Log in to reply
But because the numerator also changes, it is not enough to look at the denominator, is it?
But you are essentially right. We could notice that 1 > 2 1 and 3 2 < 3 , and deduce that 3 2 1 > 3 2 1
In the above "problem" there are no parentheses shown to show that 1 / ( 2 / 3 ) or ( 1 / 2 ) / 3 Just writing a number BIGGER doesn't mean we can "assume" the above now does it? So in my mind I read them both as 1 / ( 2 / 3 ) = 3 / 2 We should stick to BODMAS or BEDMAS rules for a strict order of mathematical operations. If you are going to diagree I suggest you try a decent scientific calculator and try sticking in a large number 1 divided by ( 2 / 3 ) with the 2 and the 3 in a smaller font or typeface size. LOL!! :-P
Log in to reply
I encourage you to learn LaTeX, and then see if you still feel the same way.
i like how this was eplained simply, compared to the other explanations.
I agree with Oliver, size does not correlate to order of operations in any math problem. This needs to be explained in the directions.
But 1 / 2 / 3 is equal to 1 / 2 / 3 no matter which colours the numbers are
Log in to reply
If you understand LaTeX, then you understand the structure of the language that is necessary to create how the problem is presented.
It would be proper to put the smaller texted fractions inside grouping symbols.
I think y griega is the answer
Let's ask the more general question: Which one is bigger, e 1 = c b a or e 2 = c b a ? I will assume that a , b , c are positive real numbers.
First, we can rewrite e 1 = b a c = c ⋅ b a ; e 2 = c 1 ⋅ b a .
Comparing the two, we see that e 1 > e 2 precisely when c > c 1 . Interestingly, the comparison only depends on the value of c ... Clearly, the last inequality is true precisely if c > 1 . Therefore we conclude
-
e 1 is greater if c > 1 ,
-
e 2 is greater if c < 1 ,
-
e 1 = e 2 if c = 1 .
In the current problem, c = 3 , so that the first option is true: the first expression is greater.
Oh this is a neat generalization.
Right, this shows that division is not associative. In general, a ÷ ( b ÷ c ) = ( a ÷ b ) ÷ c , unless c is 1 or − 1 .
Log in to reply
or (if you say "in general") c = − 1 .
Log in to reply
Oh yes, I missed that case; I have edited my comment. There's also the trivial case of a = 0 = b , c . I think those are all the possible ways in which e 1 can be equal to e 2 . Have we missed any?
Unnecessary theoretical complication; as long as C is a positive number, it is always true that c>1/c - the fraction of a number is smaller than the number itself!!!
Log in to reply
No, it isn't... For instance 1 / 2 < 1 / 2 1 = 2 . The statement c > 1 / c is true for real numbers iff either c > 1 or − 1 < c < 0 .
It might be easier for some people to conceptualise this problem by substituting the appropriate fractions with their respective decimal number.
3 2 1 = 0 . 6 ˙ 1 > 1 > 3 0 . 5 = 3 2 1
[EDIT: May 8, 2017]
Also, not for want of playing devil's advocate, but rather for a potential new understanding; Consider that the problem has been written using the LaTeX language - Toggle LaTeX in the [...] menu, or hover your cursor over the problem, and you will see that it hasn't simply been structured in a '1/2/3 or 1/2/3 ?' comparison form.
It is structured as follows (without the colors, etc.):
Which is larger, \dfrac{1}{\frac{2}{3}} or \dfrac{\frac{1}{2}}{3} ?
Once we understand how the structure of a language presents itself, we can then determine the meaning of what is presented to us when someone else uses it.
Yes, this is indeed a good way to see this. By the way 0 . 6 isn't a whole number.
The way it is written it has to be equal, there is no bigger and smaller symbol in math to inverse fraction one uses (a/b)^-1 or exactly 1/2 * 1/3 but 1/2/3 == 1/2/3 by default !!! Otherwise we end-up with some linguistic challenge: we do we put coma, so sentence is changing.
Log in to reply
I must admit that I find it a challenge to know exactly what you're saying.
When you say " The way it is written ", are you referring to the original problem, or are you referring to the way my solution is written?
I've updated my solution with an additional section, which I hope addresses the perception that we are being asked to compare 1/2/3 and 1/2/3.
One way to divide any number (n) by a fraction is to multiply n by the reciprocal of the fraction. 1 / (2/3) = 1 x (3/2) = 1.5 clearly larger than (1/2) / 3, or 1/6.
One way to divide any number (n) by a fraction is to multiply n by the reciprocal of the fraction.
Why is that so?
1 divided by something smaller than 1 is greater than 1, 1/2 divided by something greater than one is smaller than 1/2, so the answer is 1/2/3 is greater (since the result is greater than 1 and the other is smaller than 1/2)
This solution adds the parentheses which are missing in the question. Making the denominator 2/3 in a smaller green font is not the same as adding parentheses. Font size and color does not affect the order of operation. The values 1/2/3 = 1/2/3.
It really makes the solution much clearer once you fix both denominators to be the same.
First one:- 3 2 1
Second one:- 3 2 1 = 6 1
Clearly we can see that the denominator is smaller in the first one therefore the first one is the answer.
Nice, once we have made the numerators equal, we just need to look at the denominators to compare the fractions.
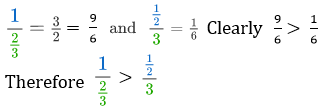
3 2 1 = 2 3 and 3 2 1 = 6 1
By comparison 2 3 is greater.