Just a Circle in a Parabola

Let the center of the circle be at $(0,a)$ and it's equation be $x^2+(y-a) ^2=1$ . Let the point of intersection of this circle and the parabola $y=x^2$ in the first quadrant be $(h, h^2)$ . Then

$h^4-(2a-1)h^2+a^2-1=0$ . Since the two curves touch each other at this point,

$(2a-1)^2=4\times 1\times (a^2-1)\implies a=\dfrac {5}{4}, h=\dfrac {\sqrt 3}{2}$ .

Hence the area of the red region is

$2\displaystyle \int_0^{\frac{\sqrt 3}{2}} (\frac{5}{4}-\sqrt {1-x^2}-x^2)dx=\dfrac{3\sqrt 3}{4}-\dfrac{π}{3}\approx \boxed {0.25184}$ .

The hint : How to you determine the intersection points between the circle and the parabola is completely meaningless.

We can solve this problem without using integration and the equation of a circle.

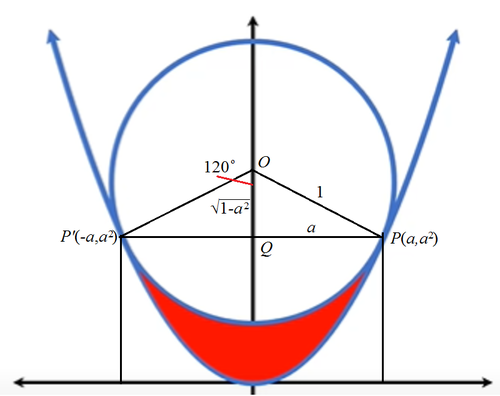
Because of symmetry, we can assume that the two points where the circle is tangent to the parabola be $P(a, a^2)$ and $P'(-a,a^2)$ . We need only consider $P(a,a^2)$ . The gradient at $P$ is $\frac {d x^2}{dx} = \frac 2x \big|_{x=a} = 2a$ . The gradient of the normal at $P$ is then $2am = - 1 \implies m = -\frac 1{2a}$ . And we note that in $\triangle OPQ$ , $\frac {\sqrt{1-a^2}}a = \frac 1{2a} \implies a = \frac {\sqrt 3}2$ .

Knowing that the area of under an inverted parabola is $\frac 23$ that of the rectangle inscribing it, the area of parabola for $y \in [0,a^2]$ , $A_p = \frac 23 (2a)a^2 = \frac 43 a^3 = \frac {\sqrt 3}2$ and the area of the red region is:

$\begin{aligned} A_{\red{\text{red}}} & = A_p - \left(\blue{\frac \pi 3} - a\sqrt{1-a^2} \right) & \small \blue{\text{Note that } \angle POP' = 120^\circ} \\ & = \frac {\sqrt 3}2 - \frac \pi 3 + \frac {\sqrt 3}4 \\ & \approx \boxed{0.252} \end{aligned}$

---

The indirect hint is to let us know that we need to find the points of tangent so that we can find the area in question.